cho tam giác ABC, dựng đường thẳng d song song với BC cắt AB,AC tại M và N sao cho AM=AN
Cho tam giác ABC có BC là cạnh dài nhất. Trên cạnh BC lấy 2 điểm D và E sao cho BD=BA, CE=CA, đường thẳng qua D song song với AB cắt AC tại M. Đường thẳng qua E song song với AC cắt AB tại N.C/m AM=AN
Ta có : DM // AB => \(\frac{AM}{AC}=\frac{BD}{BC}\) =>AM.BC =BD.AC =AB.AC
cm tương tự AN.CB =CE.AB =AC.AB
=>AM.BC =AN.CB
=>AM =AN
Cho tam giác ABC cân tại A có AB = 10cm. Lấy điểm M trên đoạn AB sao cho AM = 4cm, qua M kẻ đường thẳng d song song với BC cắt AC tại N. Tính tỉ số AN và AC?
A. 2 3
B. 1
C. 2 5
D. 2
Vì tam giác ABC cân tại A nên AB = AC = 10cm
Vì MN// BC, theo định lí Ta – let ta có:
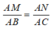
Mà AB = AC nên AM = AN = 4cm
Suy ra :

Chọn đáp án C
cho tam giác abc có ab=ac=20cm bc= 24cm. trên ab lấy m sao cho am= 4cm. qua m kẻ đường thẳng song song với bc cắt ac tại n. tính an và mn
Xét ΔABC có MN//BC
nên AM/AB=AN/AC
=>AN/20=4/20=1/5
nên AN=4(cm)
Cho tam giác ABC, trên AB lấy điểm M sao cho AM = 4cm và MB = 6cm . Qua M kẻ đường thẳng song song với BC cắt AC tại N biết AC = 20cm . Tính AN?
A. 8cm
B. 10cm
C. 12cm
D. 6cm
M nằm giữa A và B nên: AB = AM + MB = 10cm
Theo định lí Ta let ta có:
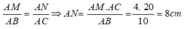
Chọn đáp án A
Cho tam giác abc có điểm m,n trên cạnh bc sao cho bm=mn=mc.Một đường thẳng song song với ac cắt ab,am,an tại d,e,f.CMR ef=3de
Hiệu số phần bằng nhau là
4 - 3 = 1 ( phần )
Chiều dài khu đất là
50 : 1 x 4 = 200 ( m )
Chiều rộng khu đất là
200 - 50 = 150 ( m )
Diện tích khu đất là
200 x 150 = 30 000 ( m2 ) = 3 ha
ĐS :
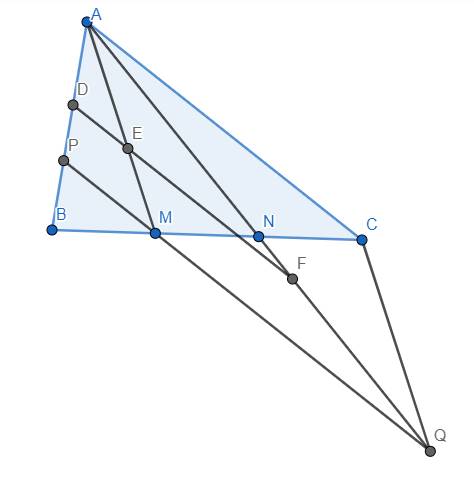
Qua M kẻ đường thẳng song song với AC cắt AB, AN lần lượt tại P và Q.
Ta thấy \(\widehat{ANC}=\widehat{QNM}\) (2 góc đối đỉnh), \(NM=NC\) (gt), \(\widehat{NCA}=\widehat{NMQ}\) (do AC//MQ) nên \(\Delta NAC=\Delta NQM\left(g.c.g\right)\)
\(\Rightarrow AC=MQ\)
Áp dụng định lý Thales trong tam giác ABC, ta có: \(\dfrac{BM}{BC}=\dfrac{PM}{AC}=\dfrac{PM}{MQ}\) \(\Rightarrow\dfrac{PM}{MQ}=\dfrac{1}{3}\)
Lại theo định lý Thales, trong tam giác APM, có: \(\dfrac{DE}{PM}=\dfrac{AE}{AM}\), trong tam giác AMQ, có \(\dfrac{AE}{AM}=\dfrac{EF}{MQ}\).
Từ đó, ta có \(\dfrac{DE}{PM}=\dfrac{EF}{MQ}\) \(\Rightarrow\dfrac{DE}{EF}=\dfrac{PM}{MQ}\). Mà \(\dfrac{PM}{MQ}=\dfrac{1}{3}\left(cmt\right)\) nên \(\dfrac{DE}{EF}=\dfrac{1}{3}\), hay \(EF=3DE\) (đpcm)
Cho tam giác ABC. M nằm trên AB sao cho AM =2/5 AB. Từ M kẻ đường thẳng song song với BC cắt AC tại N. So sánh AN và NC
Bài 3 :Cho tam giác ABC vuông tại A. Một đường thẳng song song với BC cắt 2 cạnh AB và AC theo thứ tự tại M và N; đường thẳng qua N và song song với AB, cắt BC tại D. Cho biết AM = 6, AN = 8, BM = 4.
a) Tính độ dài MN, NC và BC
b) Tính diện tích hình bình hành BMND
a) Xét ΔABC có
MN//BC(gt)
Do đó: \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)(Định lí Ta lét)
Suy ra: \(\dfrac{6}{4}=\dfrac{8}{NC}\)
hay \(NC=\dfrac{16}{3}cm\)
Ta có: AM+MB=AB(M nằm giữa A và B)
nên AB=6+4=10(cm)
Ta có: AN+NC=AC(N nằm giữa A và C)
nên \(AC=8+\dfrac{16}{3}=\dfrac{40}{3}cm\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+\left(\dfrac{40}{3}\right)^2=\dfrac{2500}{9}\)
hay \(BC=\dfrac{50}{3}cm\)
Xét ΔABC có
MN//BC(gt)
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{MN}{\dfrac{50}{3}}=\dfrac{6}{10}\)
\(\Leftrightarrow MN=\dfrac{6\cdot\dfrac{50}{3}}{10}=\dfrac{100}{10}=10cm\)
Vậy: MN=10cm; \(NC=\dfrac{16}{3}cm\); \(BC=\dfrac{50}{3}cm\)
Cho tam giác ABC kẻ EF song song với BC (E thuộc AB, F thuộc AC) sao cho AE =CF. Qua E kẻ 1 đường thẳng song song với AC cắt BC tại D a, chứng minh AD là tia phân giác của góc A b, hãy dựng 1 đường thẳng MN song song với (M thuộc AB, N thuộc AC) sao cho BM =AN c, tam giác ABC phải có điều kiện gì để tứ giác MNDB là hình thoi
Cho tam giác ABC, M lá trung điểm của AB, kẻ đường thẳng qua M song song với BC cắt AC tại N. Từ N kẻ đường thẳng song song với AB cắt BC tại P. Chứng minh rằng
a)tam giác BMN = tam giác NPB và AM = NP
b)tam giác AMN = tam giác NPC và AN = NC
huhu mình mong các bạn có thể làm nhanh lên cho mình
Câu a)
Xét tam giác ANM và tam giác CNE có :
MN = NE ( GT )
AN = NC ( GT )
góc ANM = góc CNE ( 2 góc đối đỉnh )
=> tam giác ANM = tam giác CNE ( cgc )
=> CE = AM ( cặp cạnh tương ứng )
Mà AM = BM ( do M là trung điểm AB )
=> BM = CE
Vậy BM = CE
Câu b)
Do tam giác ANM = tam giác CNE ( CMT )
=> góc MAN = góc NCE ( cặp góc tương ứng )
Mà 2 góc ở vị trí so le trong
=> AM // CE
=> góc BMC = góc MCE ( 2 góc ở vị trí so le trong )
Xét tam giác BMC và tam giác ECM có :
BM = EC ( CMT )
MC : chung
góc BMC = góc MCE ( CMT )
=> tam giác BMC = tam giác ECM ( cgc )
=> ME = BC ( cặp cạnh tương ứng )
Mà MN = ME/2 ( GT )
=> MN = BC/2
Do tam giác BMC = tam giác ECM ( CMT )
=> góc MCB = góc CME ( cặp góc tương ứng )
Mà 2 góc ở vị trí so le trong
=> ME //BC
Hay MN//BC
Vậy.....