
giúp em bài 1 và 2 đi ạ
Giúp em bài 1 và bài 2 ạ
1.
1) đúng zòi á
2) dư dấu ':', cú pháp: const tên hằng = giá trị;
3) tách ra 2 lệnh=> dấu phẩy thành ''
4) đúng r
2.
1) Biến ko đc đặt tên trùng từ khóa=> begin, start sai
2) bỏ hết dấu 2 chấm ':' đi là đúng
3) ko sai
4) thêm hai dấu ' ở giá trị xâu của hằng
=> 'Tin học'
Mong mn giúp e ạ em cần gấp mai đi học ạ em xin cảm ơn. Bài 2 ạ
a, khi cân bằng nhiệt ta có \(0,5.3,4.10^5+0,5.\left(4200+2100+400\right).t=1.\left(50-t\right).4200\Rightarrow t=5,3^oC\)
b, để nhiệt cân bằng hệ bằng 0 thì lượng nước đá p tan vừa đủ
\(m_đ.3,4.10^5=1.50.4200\Rightarrow m_đ\approx0,617\left(kg\right)\)
mong mn giúp em bài 1 và bài 2 ạ
Bài 1:
a) Ta có: \(2x-3=4x+6\)
\(\Leftrightarrow2x-4x=6+3\)
\(\Leftrightarrow-2x=9\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy: \(S=\left\{-\dfrac{9}{2}\right\}\)
Bài 1:
b) Ta có: \(\dfrac{x+2}{4}-x+3-\dfrac{1-x}{8}=0\)
\(\Leftrightarrow\dfrac{2\left(x+2\right)}{8}+\dfrac{8\left(-x+3\right)}{8}+\dfrac{x-1}{8}=0\)
Suy ra: \(2x+4-8x-24+x-1=0\)
\(\Leftrightarrow-5x-21=0\)
\(\Leftrightarrow-5x=21\)
hay \(x=-\dfrac{21}{5}\)
Vậy: \(S=\left\{-\dfrac{21}{5}\right\}\)
Bài 1: bạn tự kết luận nghiệm nhé, vì đây là những phương trình cơ bản nên mình giải tắt chút
a, \(2x-3=4x+6\Leftrightarrow-2x=9\Leftrightarrow x=-\dfrac{9}{2}\)
b, \(\dfrac{x+2}{4}+3-\dfrac{1-x}{8}=0\)
\(\Leftrightarrow\dfrac{2x+4+24-1+x}{8}=0\Rightarrow3x+27=0\Leftrightarrow x=-3\)
c, \(x\left(x-1\right)+x\left(x+3\right)=0\Leftrightarrow x^2-x+x^2+3x=0\)
\(\Leftrightarrow2x^2+2x=0\Leftrightarrow2x\left(x+1\right)=0\Leftrightarrow x=0;x=-1\)
d, \(\dfrac{x}{2x-6}-\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)ĐK : \(x\ne-1;3\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}-\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{x^2+x-x^2+3x}{2\left(x+1\right)\left(x-3\right)}=\dfrac{4x}{2\left(x+1\right)\left(x-3\right)}\Rightarrow0=0\)
Vậy phương trình có vô số nghiệm
Mn ơi giúp em làm bài 3 và bài 4 với ạ,mai đi học rồi mà em ko bt Làm:((
3)
a)vì góc E=F=40 mà 2 góc có vị trí đồng vị
b)vì góc F=M=40 mà 2 góc có vị trí so le ngoài
b//c mà b//a suy ra a//c
4)
a)vì góc A1=B1 mà 2 góc có vị trí đồng vị
b)B4=B1, A3=A1
vì B1+B2=180 suy ra B2=110=B3 đối đỉnh
A2=A4=110
Bài 3: (gọi tạm hai góc có trong hình là E1 và F1)
a/ Ta có: \(\hat{E_1}=\hat{F_1}=40\text{°}\)
- Hai góc ở vị trí đồng vị. Vậy:\(a\text{ // }b\)
-------------------
b/ Gọi góc đối đỉnh F1 là F2
- \(F_1=F_2=40\text{°}\) (đối đỉnh)
- \(F_2=M_1=40\text{°}\). Mà F2 và M1 là hai góc đồng vị
⇒\(b\text{ // }c\)
- \(a\text{ // }b\); \(b\text{ // }c\)
Vậy: \(a\text{ // }c\)
==========
Bài 4:
a/ \(A_1=B_1=70\text{°}\text{ }\)
- Mà A1 và B1 là hai góc đồng vị. Vậy: \(a\text{ // }b\)
--------------------
b/ \(\hat{A_2}=180\text{}\text{°}-\hat{A_1}=130\text{°}\) (kề bù)
\(\hat{A_3}=\hat{A_1}=70\text{°}\)(đối đỉnh)
\(\hat{A_4}=\hat{A_2}=130\text{°}\) (đối đỉnh)
\(\hat{B_2}=180\text{°}-\hat{A_1}=130\text{°}\) (trong cùng phía)
\(\hat{B_3}=\hat{B_2}=130\text{°}\) (đối đỉnh)
\(\hat{B_4}=\hat{A_1}=70\text{°}\) (so le trong)
Chúc bạn học tốt
Giúp em bài 1 và 2 ạ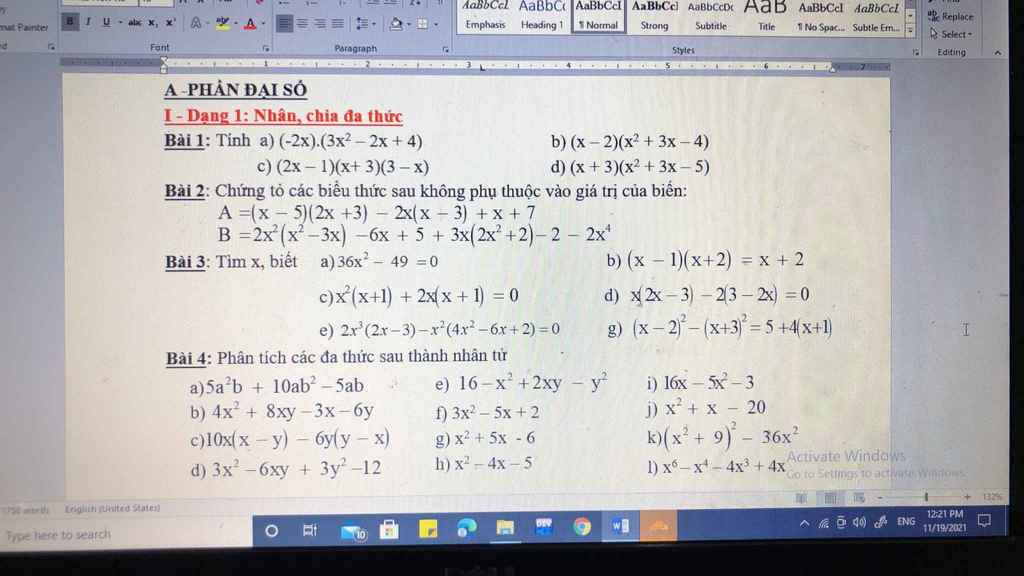
Bài 1:
\(a,\left(-2x\right)\left(3x^2-2x+4\right)=-6x^3+4x^2-8x\\ b,\left(x-2\right)\left(x^2+3x-4\right)=x\left(x^2+3x-4\right)-2\left(x^2+3x-4\right)=x^3+3x^2-4x-2x^2-6x+8=x^3+x^2-10x+8\)
\(c,\left(2x-1\right)\left(x+3\right)\left(3-x\right)=\left(2x-1\right)\left(9-x^2\right)=9\left(2x-1\right)-x^2\left(2x-1\right)=18x-9-2x^3+x^2\\ d,\left(x+3\right)\left(x^2+3x-5\right)=x\left(x^2+3x-5\right)+3\left(x^2+3x-5\right)=x^3+3x^2-5x+3x^2+9x-15=x^3+6x^2+4x-15\)
Bài 2:
\(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\\ =2x^2-10x+3x-15-2x^2+6x+x+7\\ =-8\)
\(B=2x^2\left(x^2-3x\right)-6x+5+3x\left(2x^2+2\right)-2-2x^4\\ =2x^4-6x^3-6x+5+6x^3+6x-2-2x^4\\ =3\)
Vậy A,B không phụ thuộc vào giá trị của biến
Thầy cô giúp em bài 2 ý 1 và 3 với ạ, em đang cần gấp ạ 
3) Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m^2-6\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-6\right)\)
\(=4m^2-8m+4-4m^2+24\)
\(=-8m+28\)
Để phương trình có hai nghiệm phân biệt x1;x2 thì Δ>0
\(\Leftrightarrow-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{1}=2m-2\\x_1x_2=m^2-6\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=16\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-6\right)-16=0\)
\(\Leftrightarrow4m^2-8m+4-2m^2+12-16=0\)
\(\Leftrightarrow2m^2-8m=0\)
\(\Leftrightarrow2m\left(m-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\left(nhận\right)\\m=4\left(loại\right)\end{matrix}\right.\)
Giúp em bài 1 và 2 với bài nào cũng được ạ
Câu 2:
a: Ta có: \(25x^2-9=0\)
\(\Leftrightarrow\left(5x-3\right)\left(5x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-\dfrac{3}{5}\end{matrix}\right.\)
b: Ta có: \(\left(x-4\right)^2-\left(x-2\right)\left(x+2\right)=6\)
\(\Leftrightarrow x^2-8x+16-x^2+4=6\)
\(\Leftrightarrow-8x=-14\)
hay \(x=\dfrac{7}{4}\)
c: Ta có: \(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x-7\right)\left(x+7\right)=0\)
\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5\left(x^2-49\right)=0\)
\(\Leftrightarrow5x^2+2x+10-5x^2+245=0\)
\(\Leftrightarrow x=-\dfrac{255}{2}\)
GIÚP EM Ý D,E BÀI 1 VÀ BÀI 2 VỚI Ạ
d: \(\Leftrightarrow x^2-x-1=x+2\)
\(\Leftrightarrow x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
e: \(\Leftrightarrow x^2-x-2+x-1=3x+4\)
\(\Leftrightarrow x^2-3-3x-4=0\)
\(\Leftrightarrow x^2-3x-7=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-7\right)=37\)
Vì Δ>0 nên pt có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{37}}{2}\\x_2=\dfrac{3+\sqrt{37}}{2}\end{matrix}\right.\)
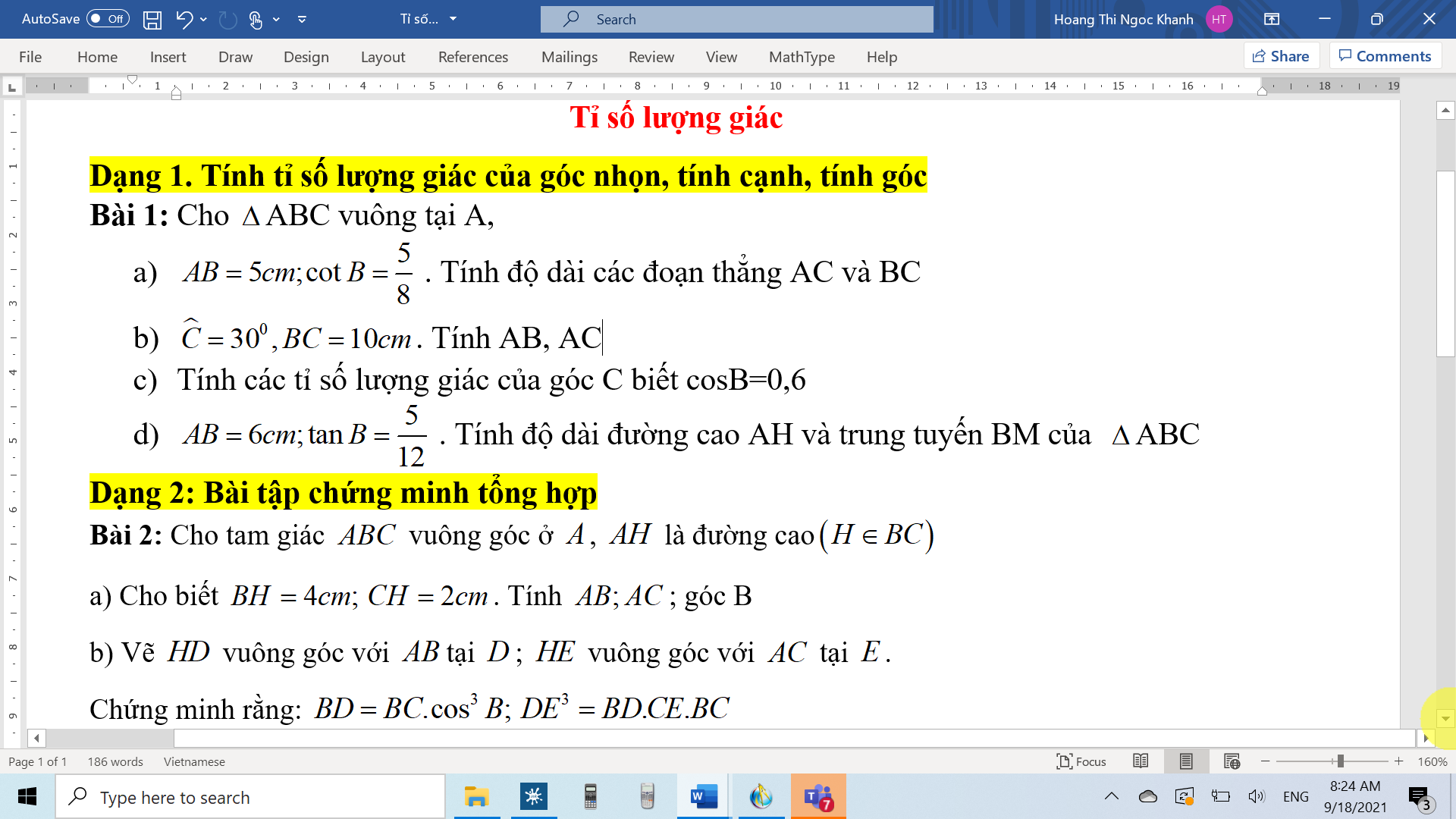
giúp em câu b bài 1 và ý 2 câu b bài 2 ạ