xét sự biến thiên của sin(pi/3-2x) voi x thuoc (-pi/2;pi/2)
KD
Những câu hỏi liên quan
Cho cos2x=-\(\dfrac{4}{5}\), voi \(\dfrac{\pi}{4}< x< \dfrac{\pi}{2}\). Tinh sinx, cosx, sin(x+\(\dfrac{\pi}{3}\)), cos(2x-\(\dfrac{\pi}{4}\)).
Lời giải:
$-\frac{4}{5}=\cos 2x=2\cos ^2x-1$
$\Leftrightarrow \cos ^2x=\frac{1}{10}$
Vì $x\in (\frac{\pi}{4}; \frac{\pi}{2})$ nên $\cos x>0$
$\Rightarrow \cos x=\sqrt{\frac{1}{10}}$
$\sin^2x=1-\cos ^2x=\frac{9}{10}$
Vì $x\in (\frac{\pi}{4}; \frac{\pi}{2})$ nên $\sin x>0$
$\Rightarrow \sin x=\frac{3}{\sqrt{10}}$
$\sin (x+\frac{\pi}{3})=\sin x\cos \frac{\pi}{3}+\cos x\sin \frac{\pi}{3}$
$=\sqrt{\frac{9}{10}}.\frac{1}{2}+\sqrt{\frac{1}{10}}.\frac{\sqrt{3}}{2}=\frac{\sqrt{30}+3\sqrt{10}}{20}$
Đúng 2
Bình luận (1)
Xét sự đồng biến, nghịch biến của các hàm số :
a) \(y=x-\sin x,x\in\left[0;2\pi\right]\)
b) \(y=x+2\cos x,x\in\left[\dfrac{\pi}{6};\dfrac{5\pi}{6}\right]\)
c) \(y=\sin\dfrac{1}{x},x>0\)
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { - 20\pi ; - 19\pi } \right),\left( { - 9\pi ; - 8\pi } \right)\)
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
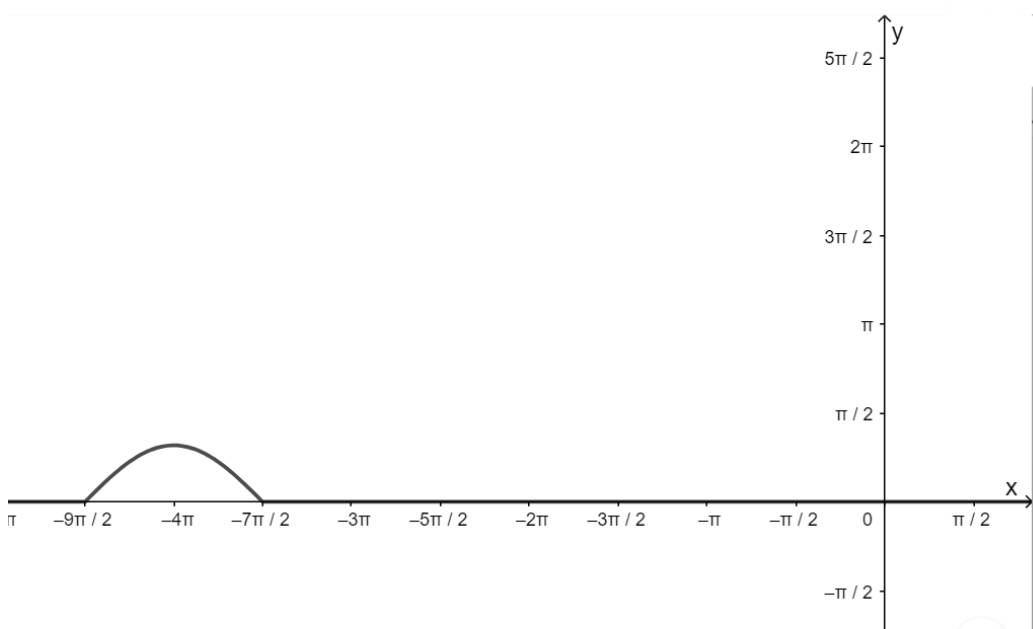
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
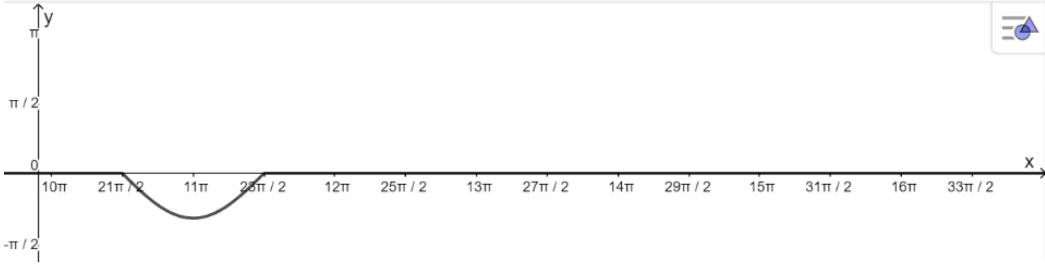
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
Đúng 0
Bình luận (0)
cho hàm số y f(x) 2sin2x .a) chứng minh rằng với số nguyên k tùy ý , luôn có f(x + kpi) f(x) với mọi x .b) lập bảng biến thiên của hàm số y 2sin2x trên đoạn left[-frac{pi}{2};frac{pi}{2}right]c) vẽ đồ thị của hàm số y 2sin2x .
Đọc tiếp
cho hàm số y = f(x) = 2\(\sin\)2x .
a) chứng minh rằng với số nguyên k tùy ý , luôn có f(x + k\(\pi\)) = f(x) với mọi x .
b) lập bảng biến thiên của hàm số y = 2\(\sin\)2x trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
c) vẽ đồ thị của hàm số y = 2\(\sin\)2x .
cho hàm số y = f(x) = 2\(\sin\)2x .
a) lập bảng biến thiên của hàm số y = 2\(\sin\)2x trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
b) vẽ đồ thị của hàm số y = 2\(\sin\)2x .
Xét tính chẵn, lẻ của các hàm số1,ycosx+sin^2x2,ysinx+cosx3,ytanx+2sinx4,ytan2x-sin3x5,sin2x+cosx6,ycosx.sin^2x-tan^2x7,ycosleft(x-dfrac{pi}{4}right)+cosleft(x+dfrac{pi}{4}right)8,ydfrac{2+cosx}{1+sin^2x}9,yleft|2+sinxright|+left|2-sinxright|
Đọc tiếp
Xét tính chẵn, lẻ của các hàm số
1,\(y=cosx+sin^2x\)
2,\(y=sinx+cosx\)
3,\(y=tanx+2sinx\)
4,\(y=tan2x-sin3x\)
5,\(sin2x+cosx\)
6,\(y=cosx.sin^2x-tan^2x\)
7,\(y=cos\left(x-\dfrac{\pi}{4}\right)+cos\left(x+\dfrac{\pi}{4}\right)\)
8,\(y=\dfrac{2+cosx}{1+sin^2x}\)
9,\(y=\left|2+sinx\right|+\left|2-sinx\right|\)
Chứng minh tính đơn điệu của hàm số y=sin x đồng biến trên khoảng (\(\dfrac{-\pi}{2}+k2\pi;\dfrac{\pi}{2}+k2\pi\)) và nghịch biến trên khoảng (\(\dfrac{\pi}{2}+k2\pi;\dfrac{3\pi}{2}+k2\pi\))
Trên \(\left(-\dfrac{\pi}{2}+k.2\pi;\dfrac{\pi}{2}+k.2\pi\right)\) chọn 2 giá trị của x (x1 và x2) sao cho x1 > x2
Xét f(x1) - f(x2) = sinx1 - sinx2
= 2cos\(\dfrac{x_1+x_2}{2}\) . sin \(\dfrac{x_1-x_2}{2}\)
Do \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)
⇒ cos\(\dfrac{x_1+x_2}{2}\) > 0
Mà \(sin\dfrac{x_1-x_2}{2}\) > 0
nên f(x1) - f(x2) > 0
Vậy đồng biến
Nghịch biến tương tự
Đúng 0
Bình luận (4)
rút gọn biểu thức:
A= cosa.sin( b-c )+ cosb. sin(c-a) + cosc.sin( a-b)
B= \(sin^2x+cos\left(\frac{\pi}{3}-x\right).cos\left(\frac{\pi}{3}+x\right)\)
C=\(sin^2x+sin^2\left(\frac{2\pi}{3}+x\right)+sin^2\left(\frac{2\pi}{3}-x\right)\)
D=\(sin^2\left(\frac{\pi}{4}+x\right)-sin^2x-2sinx.sin\frac{\pi}{4}.cos\left(\frac{\pi}{4}+x\right)\)
\(A=cosa\left(sinb.cosc-cosb.sinc\right)+cosb\left(sinc.cosa-cosc.sina\right)+cosc\left(sinacosb-cosasinb\right)\)
\(A=cosasinbcosc-cosacosbsinc+cosacosbsinc-sinacosbcosc+sinacosbcosc-cosasinbcosc\)
\(A=0\)
\(B=sin^2x+\frac{1}{2}\left(cos\frac{2\pi}{3}+cos2x\right)\)
\(B=\frac{1}{2}-\frac{1}{2}cos2x-\frac{1}{4}+\frac{1}{2}cos2x\)
\(B=\frac{1}{4}\)
\(C=\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos\left(\frac{4\pi}{3}+2x\right)+\frac{1}{2}-\frac{1}{2}cos\left(\frac{4\pi}{3}-2x\right)\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x-\frac{1}{2}\left(cos\left(\frac{4\pi}{3}+2x\right)+cos\left(\frac{4\pi}{3}-2x\right)\right)\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x-cos\frac{4\pi}{3}.cos2x\)
\(C=\frac{3}{2}-\frac{1}{2}cos2x+\frac{1}{2}cos2x\)
\(C=\frac{3}{2}\)
\(D=\frac{1}{2}\left[\sqrt{2}sin\left(\frac{\pi}{4}+x\right)\right]^2-sin^2x-sinx.\sqrt{2}cos\left(\frac{\pi}{4}+x\right)\)
\(D=\frac{1}{2}\left(sinx+cosx\right)^2-sin^2x-sinx\left(sinx-cosx\right)\)
\(D=\frac{1}{2}\left(1+2sinx.cosx\right)-sin^2x-sin^2x+sinx.cosx\)
\(D=\frac{1}{2}+sinxcosx+sinxcosx=\frac{1}{2}+sin2x\)
Đúng 0
Bình luận (0)
Góc độ cao của thang dựa vào tường là 60º và chân thang cách tường 4,6 m. Chiều dài của thang là
Đúng 0
Bình luận (0)
Tìm đạo hàm các hàm số:
1, \(y=\tan(3x-\dfrac{\pi}{4})+\cot(2x-\dfrac{\pi}{3})+\cos(x+\dfrac{\pi}{6})\)
2, \(y=\dfrac{\sqrt{\sin x+2}}{2x+1}\)
3, \(y=\cos(3x+\dfrac{\pi}{3})-\sin(2x+\dfrac{\pi}{6})+\cot(x+\dfrac{\pi}{4})\)
a.
\(y'=\dfrac{3}{cos^2\left(3x-\dfrac{\pi}{4}\right)}-\dfrac{2}{sin^2\left(2x-\dfrac{\pi}{3}\right)}-sin\left(x+\dfrac{\pi}{6}\right)\)
b.
\(y'=\dfrac{\dfrac{\left(2x+1\right)cosx}{2\sqrt{sinx+2}}-2\sqrt{sinx+2}}{\left(2x+1\right)^2}=\dfrac{\left(2x+1\right)cosx-4\left(sinx+2\right)}{\left(2x+1\right)^2}\)
c.
\(y'=-3sin\left(3x+\dfrac{\pi}{3}\right)-2cos\left(2x+\dfrac{\pi}{6}\right)-\dfrac{1}{sin^2\left(x+\dfrac{\pi}{4}\right)}\)
Đúng 2
Bình luận (0)





