1. Cho △ABC có A(2;4), B(5;1), C(-1;-2). Phép tịnh tiến TBC biến tam giác ABC thành tam giác A'B'C'. Tìm tọa độ trọng tâm của tam giác A'B'C'.
HN
Những câu hỏi liên quan
Câu 1:
1) Cho tam giác ABC có góc A = góc C-10độ; góc B=góc C + 10độ. Tính các góc của tam giác ABC?
2) Cho tam giác ABC có góc B= 7/6 góc C; góc A= 5/6 góc C. Tính các góc của tam giác ABC?
3) cho tam giác ABC có góc A= 2. Góc B ; góc B = góc C . tính các góc của tam giác ABC?
4) Cho tam giác ABC có góc A= 5.góc C; góc B= 2.góc C. tínhcác góc của tam giác ABC?
cho \(\Delta ABC\) có A(1;-2) B(3;0) C(-2;-1). tính diện tích \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(2,2\right)\\\overrightarrow{BC}=\left(-5,-1\right)\\\overrightarrow{AC}=\left(-3,1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{2^2+2^2}=2\sqrt{2}\\BC=\sqrt{\left(-5\right)^2+\left(-1\right)^1}=\sqrt{26}\\AC=\sqrt{\left(-3\right)^2+1^2}=\sqrt{10}\end{matrix}\right.\)
\(p=\dfrac{2\sqrt{2}+\sqrt{26}+\sqrt{10}}{2}\)
Áp dụng công thức Herong:
\(S=\sqrt{p.\left(p-2\sqrt{2}\right)\left(p-\sqrt{26}\right)\left(p-\sqrt{10}\right)}=\sqrt{16}=4\)
Đúng 1
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
Cho tam giác ABC có A(-1; 1), B(0; 2), C(1; 1). Trực tâm của tam giác ABC có tọa độ là
A.(0; 2)
B. (0; 1)
C. (1; 0)
D. (1; 1)
Gọi tọa độ điểm H(a;b)
Ta có: A H → = a + 1 ; b − 1 , B H → = a ; b − 2 , B C → = 1 ; − 1 , A C → 2 ; 0
Do H là trực tâm tam giác ABC nên:
A C → . B H → = 0 B C → . A H → = 0 ⇒ 2. a + 0. b − 2 = 0 1. a + 1 − 1. b − 1 = 0 ⇒ a = 0 b = 2
Vậy H (0; 2).
Chọn A
Đúng 0
Bình luận (0)
1.Cho tam giác ABC,có BM và CN là đường phân giác.CMR:1/BC+1/AB=1/MN
2.Cho tam giác ABC cân tại A, góc A=36 độ.CMR AB^2=BC^2+AC.BC
1 cho △ABC thỏa mãn: 2cos B= √2.Khi đó B=?2 cho △ABC có C^=45 độ,B^=75 độ số đo góc A là bao nhiêu3 cho △ABC có s=84,a=13,b=14,c=15 độ dài bán kính đường tròn ngoại tiếp r của △ trên là?
Xem chi tiết
1. \(2cosB=\sqrt{2}\Rightarrow cosxB=\dfrac{\sqrt{2}}{2}\Rightarrow B=45^0\)
2. \(A=180^0-\left(B+C\right)=60^0\)
3. \(r=\dfrac{S}{p}=\sqrt{3}\)
4. \(R=\dfrac{abc}{4S}=\dfrac{65}{8}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có A(5;3) : B(2;-1) và C(-1; 5). Tính diện tích tam giác ABC.
A. 5
B. 10
C. 15
D. 20
Chọn C.
Gọi A’ là chân đường cao kẻ từ A.
Theo câu 64 ta có tọa độ điểm A’ là A’(1;1)
Ta có
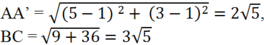
Suy ra ![]()
Đúng 0
Bình luận (0)
Bài 1:1. Cho DeltaABC vuông tại A. Có AB bằng frac{1}{2}BC. Tính góc C?2. Cho DeltaABC vuông tại A. Có góc B30 độ. C/m ACfrac{1}{2}BC3. Cho DeltaABC. Có trung tuyến BMCN. C/m DeltaABC cân tại A.4. Cho DeltaABC có trung tuyến AM đồng thời là đường phân giác góc A. C/m DeltaABC cân tại A.Giúp mk nhé mai phải nộp rùi!!!
Đọc tiếp
Bài 1:
1. Cho \(\Delta\)ABC vuông tại A. Có AB bằng \(\frac{1}{2}\)BC. Tính góc C?
2. Cho \(\Delta\)ABC vuông tại A. Có góc B=30 độ. C/m AC=\(\frac{1}{2}\)BC
3. Cho \(\Delta\)ABC. Có trung tuyến BM=CN. C/m \(\Delta\)ABC cân tại A.
4. Cho \(\Delta\)ABC có trung tuyến AM đồng thời là đường phân giác góc A. C/m \(\Delta\)ABC cân tại A.
Giúp mk nhé mai phải nộp rùi!!!
Bài 1:
Gọi M là trung điểm của BC
Vẽ BE là tia phân giác của góc B, E thuộc AC
nối M với E
ta có: BM =CM = 1/2.BC ( tính chất trung điểm)
AB=1/2.BC (gt)
=> BM = CM= AB ( =1/2.BC)
Xét tam giác ABE và tam giác MBE
có: AB = MB (chứng minh trên)
góc ABE = góc MBE (gt)
BE là cạnh chung
\(\Rightarrow\Delta ABE=\Delta MBE\left(c-g-c\right)\)
=> góc BAE = góc BME = 90 độ ( 2 cạnh tương ứng)
=> góc BME = 90 độ
\(\Rightarrow BC\perp AM⋮M\)
Xét tam giác BEM vuông tại M và tam giác CEM vuông tại M
có: BM=CM(gt)
EM là cạnh chung
\(\Rightarrow\Delta BEM=\Delta CEM\left(cgv-cgv\right)\)
=> góc EBM = góc ECM ( 2 cạnh tương ứng)
mà góc EBM = góc ABE = 1/2. góc B (gt)
=> góc EBM = góc ABE = góc ECM
Xét tam giác ABC vuông tại A
có: \(\widehat{B}+\widehat{ECM}=90^0\) ( 2 góc phụ nhau)
=> góc EBM + góc ABE + góc ECM = 90 độ
=> góc ECM + góc ECM + góc ECM = 90 độ
=> 3.góc ECM = 90 độ
góc ECM = 90 độ : 3
góc ECM = 30 độ
=> góc C = 30 độ
Đúng 0
Bình luận (0)
1.Cho tam giác ABC cân đỉnh A, góc BAx là góc ngoài tại đỉnh A của tam giác ABC. Chứng minh rằng góc BAx bằng 2.B
2.Cho tam giác ABC có góc A bằng 90, góc B bằng 60. Chứng minh rằng AB = 1/2 BC.


