cho hình bình hành ABCD đường chéo AC=30 góc a=140 độ. Tính AD,AB
Cho hình bình hành có ABCD có AC = 8 cm ; DB = 10 cm , Hai đường chéo AC và BD tạo nhau góc 30 độ , Tính diện tích hình bình hành ABCD
cho hình bình hành ABCD, đường chéo AC lớn hơn đường chéo BD. Kẻ CH vuông góc với AD, CK vuông góc với AB
, Tính diện tích am giác CKH ,tứ giác AKCH nếu góc BAD=60, AB=4cm,AD=5cm
cho hình bình hành ABCD có AC > BD . Vẽ CE vuông góc với AB tại E và CF vuông góc với AD tại F . Biết đường chéo AC = a , hãy tính AB.AE + AD.AF theo a .
2. Cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo BD, kẻ CH vuông góc AD, CK vuông góc AB
a) Chứng minh tam giác CKH đồng dạng tam giác BCA
b) Chứng minh HK=Ac.sinBAD
c) Tính diện tích tứ giác AKCH nếu góc BAD = 60 độ, AB=4cm, AD=5cm
GIẢI:
a) Chứng minh tam giác CKH đồng dạng tam giác BCA
AKC^ + ABC^ = 2v => AKCH nội tiếp
=> CHK^ = CAB^ (1) ( cùng chắn cung CK)
CKH^ = CAH^ (2) ( cùng chắn cung CH)
CAH^ = ABC^ (3) ( so le trong)
(2) và (3) => CKH^ = ACB^ (4)
(1) và (4) => ΔCKH ~ ΔBCA (g.g)
b) Chứng minh HK=AC.sinBAD
ΔCKH ~ ΔBCA =>HK/AC = CH/AB = CH/CD = sin(CDH^) = sin(BAD^) ( đồng vị)
=> HK = AC.sin(BAD^)
c) Tính diện tích tứ giác AKCH nếu góc BAD = 60 độ, AB=4cm, AD=5cm
AB = CD = 4
CDH^ = BAD^ = 60*
=> CH = 4√3/2 = 2√3 ( đường cao tam giác đều cạnh = 4)
DH = CD/2 = 4/2 = 2
=> AH = AD + DH = 5 + 2 = 7
AD = BC = 5
CBK^ = BAD^ = 60*
=> CK = 5.√3/2
BK = BC/2 = 5/2
=> AK = AB + BK = 4 + 5/2 = 13/2
S(AKCH) = S(ACK) + S(ACH) = AK.CK/2 + AH.CH/2
= (13/2).( 5.√3/2)/2 + 7.(2√3)/2 = 732√3/8
chúc bạn học tốt
hình bình hành ABCD có cạnh AB=4, hai đường chéo AC=6 và BD=8. Tính độ dài cạnh AD
Gọi O là giao của hai đường chéo
Ta có: \(\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}\); \(\overrightarrow{AD}=\overrightarrow{AO}+\overrightarrow{OD}=\overrightarrow{AO}-\overrightarrow{OB}\)
Suy ra : \(\overrightarrow{AB}.\overrightarrow{AD}=AO^2-OB^2=3^2-4^2=-7\)
\(\Leftrightarrow AB^2.AD^2=49\)\(\Leftrightarrow AD^2=\dfrac{49}{16}\Leftrightarrow AD=\dfrac{7}{4}\)
Hình bình hành ABCD có độ dài cạnh AB = a = 12,5cm, BC = b = 7,25cm. Đường phân giác của góc B cắt đường chéo AC tại E, đường phân giác của góc D cắt đường chéo AC tại F
Hãy tính độ dài đường chéo AC, biết EF = m = 3,45cm.
(Tính chính xác đến hai chữ số thập phân)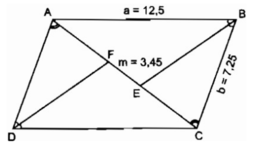
Vì ABCD là hình bình hành nên ∠ ABC = ∠ ADC.
Mặt khác, BE và DF lần lượt là phân giác của các góc B và D, do đó suy ra ∠ ADF = ∠ CBE
Mặt khác, ta có: AD = CB = b;
∠ DAF = ∠ BCE (so le trong)
Suy ra: △ ADF = △ CBE (g.c.g)
⇒ AF = CE
Đặt AF = CE = x
Theo tính chất của đường phân giác BE trong tam giác ABC, ta có: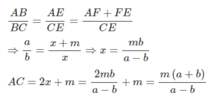
Thay số, tính trên máy tính điện tử cầm tay ta được: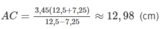
Cho hình bình hành ABCD biết AB = 5 AD = 9 và đường chéo BD = 11 tính AC
Bài 2 : Cho hình bình hành ABCD, có đường chéo lớn AC. Từ C kẻ CE vuông góc AB, CF vuông góc AD ; BH vuông góc AC. Chứng minh : a) AB.AE = AH.AC b) BC.AF = AC.HC c) AB.AE + AD.AF = AC2 . d) Cho biết CE = 16cm, CF = 20cm, chu vi ABCD = 108cm. Tính diện tích ABCD
Giúp mk vs khó quá
Dựng BG ⊥ AC.
Xét ∆ BGA và ∆ CEA, ta có:
ˆBGA=ˆCEA=90∘BGA^=CEA^=90∘
ˆAA^ chung
Suy ra: ∆ BGA đồng dạng ∆ CEA (g.g)
Suy ra: ABAC=AGAEABAC=AGAE
Suy ra: AB.AE = AC.AG (1)
Xét ∆ BGC và ∆ CFA, ta có:
ˆBGC=ˆCFA=90∘;BGC^=CFA^=90∘
ˆBCG=ˆCAF;BCG^=CAF^ (so le trong vì AD // BC)
Suy ra: ∆ BGC đồng dạng ∆ CFA (g.g)
Suy ra: AFCG=ACBC⇒BC.AF=AC.CGAFCG=ACBC⇒BC.AF=AC.CG
Mà BC = AD (tính chất hình bình hành )
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế của đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
⇒AB.AE+AD.AF=AC(AG+CG)⇒AB.AE+AD.AF=AC(AG+CG)
Mà AG+CG=ACAG+CG=AC nên AB.AE+AD.AF=AC2
Bài 1 : Hình thoi ABCD có góc B = 120 và AB = 5 cm . Khi đó độ dài đoạn BD là :
Bài 2 : Cho hình thang ABCD có cạnh = 2 cm , góc A = 60 . Khi đó độ dài đường chéo AC của hình thang là :
Bài 3 : Cho hình bình hành ABCD có góc A = 2 . góc B và AD = AB . Khi đó số đo của góc BAC là
Bai 1:
Ta co: BD la duong cheo vua la duong phan giac ( T/c cua duong cheo trong hinh thoi )
Thay co goc B = 120 cm, suy ra goc ABC = 60 do
Tam giac ABC la tam giac deu
AB = AD = BD = 5