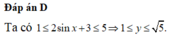giá trị lớn nhất của hàm số y=2sinx-4/3 sin^3 x trên [0;π]
ND
Những câu hỏi liên quan
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 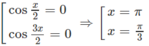
Ta có: f(0) = 0,
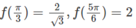
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= sin^2x +2sinx
Đặt \(sinx=t\in\left[-1;1\right]\)
\(y=f\left(t\right)=t^2+2t\)
Xét hàm \(y=f\left(t\right)=t^2+2t\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-1;1\right]\)
\(f\left(-1\right)=-1\) ; \(f\left(1\right)=3\)
\(\Rightarrow y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
Đúng 2
Bình luận (0)
cho hàm số y = 2sinx - 4 tìm giá trị lớn nhất và nhỏ nhất của hàm số trên R
\(-1\le sinx\le1\Rightarrow2.\left(-1\right)-4\le y\le2.1-4\)
\(\Rightarrow-6\le y\le-2\)
\(y_{min}=-6\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=1\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất nhỏ nhất
a, y=\(sin^2x-2sinx+3cos^2x\) trên \(\left[0;\dfrac{\Pi}{2}\right]\)
b,\(y=sinx-cosx+sin2x+5\) trên \(\left[0;\dfrac{\Pi}{4}\right]\)
c,\(y=sinx-cosx+sinxcosx-3\)
a, \(y=sin^2x-2sinx+3cos^2x\)
\(=sin^2x-2sinx+3\left(1-sin^2x\right)\)
\(=3-2sinx-2sin^2x\)
Đặt \(sinx=t\left(t\in\left[0;1\right]\right)\)
\(\Rightarrow y=f\left(t\right)=3-2t-2t^2\)
\(\Rightarrow y_{min}=min\left\{f\left(0\right);f\left(1\right)\right\}=-1\)
\(y_{max}=max\left\{f\left(0\right);f\left(1\right)\right\}=3\)
Đúng 0
Bình luận (0)
b, \(y=sinx-cosx+sin2x+5\)
\(=sinx-cosx-\left(sinx-cosx\right)^2+6\)
Đặt \(sinx-cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(\Rightarrow y=f\left(t\right)=-t^2+t+6\)
\(\Rightarrow y_{min}=min\left\{f\left(-\sqrt{2}\right);f\left(0\right)\right\}=4-\sqrt{2}\)
\(y_{max}=max\left\{f\left(-\sqrt{2}\right);f\left(0\right)\right\}=6\)
Đúng 0
Bình luận (0)
c, \(y=sinx-cosx+sinx.cosx-3\)
\(=sinx-cosx-\dfrac{1}{2}\left(sinx-cosx\right)^2-\dfrac{5}{2}\)
Đặt \(sinx-cosx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\)
\(\Rightarrow y=f\left(t\right)=-\dfrac{1}{2}t^2+t-\dfrac{5}{2}\)
\(\Rightarrow y_{min}=min\left\{f\left(-\sqrt{2}\right);f\left(\sqrt{2}\right);f\left(1\right)\right\}=-\dfrac{7+2\sqrt{2}}{2}\)
\(y_{max}=max\left\{f\left(-\sqrt{2}\right);f\left(\sqrt{2}\right);f\left(1\right)\right\}=-2\)
Đúng 0
Bình luận (0)
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
3
sin
x
+
2
sin
x
+
1
trên đoạn
0
;
π
2
. Khi đó giá trị của...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 3 sin x + 2 sin x + 1 trên đoạn 0 ; π 2 . Khi đó giá trị của M 2 + m 2 là
A. 31 2
B. 11 2
C. 41 4
D. 61 4
Chọn C
Đặt ![]()
Xét hàm ![]() trên đoạn [0;1] có
trên đoạn [0;1] có 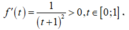
Suy ra hàm số đồng biến trên [0;1]
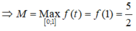 và
và ![]()
Khi đó, 
Đúng 0
Bình luận (0)
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
2
sin
x
+
3
A.
m
a
x
y
5
,
m
i
n
y
2
B.
m
a
x
y
5
,
m
i
n
y...
Đọc tiếp
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 2 sin x + 3
A. m a x y = 5 , m i n y = 2
B. m a x y = 5 , m i n y = 3
C. m a x y = 5 , m i n y = 1
D. m a x y = 5 , m i n y = 2 5
Giá trị nhỏ nhất và lớn nhất của hàm số
y
2
sin
x
+
cos
x
+
3
-
sin
x
+
2
cos
+
4
lần lượt là: A. 1/2 và 1 B. 1/2 và 2 C. 2/11 và 1 D. 2/11 và 2
Đọc tiếp
Giá trị nhỏ nhất và lớn nhất của hàm số y = 2 sin x + cos x + 3 - sin x + 2 cos + 4 lần lượt là:
A. 1/2 và 1
B. 1/2 và 2
C. 2/11 và 1
D. 2/11 và 2
Xét − sin x + 2 cos x + 4 = 0
Ta thấy − 1 2 + 2 2 < 4 2 nên phương trình vô nghiệm.
Do đó − sin x + 2 cos x + 4 ≠ 0 .
Như vậy, y = 2 sin x + cos x + 3 − sin x + 2 cos x + 4
⇔ y − sin x + 2 cos x + 4 = 2 sin x + cos x + 3
⇔ sin x 2 + y + cos x 1 − 2 y + 3 − 4 y = 0
Để phương trình có nghiệm thì 2 + y 2 + 1 − 2 y 2 ≥ 3 − 4 y 2
⇔ 5 y 2 + 5 ≥ 16 y 2 − 24 y + 9
⇔ 11 y 2 − 24 y + 4 ≤ 0
⇔ 2 11 ≤ y ≤ 2
Chọn đáp án D.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của hàm số: y = 3 - 2sinx
Ta có: -1 ≤ sin x ≤ 1
⇒ -2 ≤ -2sin x ≤ 2
⇒ 1 ≤ 3 – 2sin x ≤ 5
hay 1 ≤ y ≤ 5.
Vậy hàm số đạt giá trị lớn nhất bằng 5.
Đúng 0
Bình luận (0)