Giúp mk vs mk cần gấp
X2.(x2+4)-X2 - 4
Thanks mn
cho x,y thoả mãn : x3+2y2-4y +3=0
x2+x2y2-2y=0
tính Q=x2+y2
nhờ mn giúp mk vs ạ
mình đang cần gấp
\(\Leftrightarrow\left\{{}\begin{matrix}x^3+2y^2-4y+3=0\\2x^2+2x^2y^2-4y=0\left(1\right)\end{matrix}\right.\Rightarrow}x^3+2y^2-4y-2x^2-2x^2y^2+4y=0\Rightarrow x^3+1-2x^2y^2+2y^2-2x^2+2=0\Rightarrow\left(x+1\right)\left(x^2-x+1\right)-2y^2\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(x^2-x+1-2xy^2+2y^2-2x+2\right)=0\Rightarrow x=-1\)Thay x=-1 vào (1) ta được y2-2y+1=0⇒ (y-1)2=0⇒y-1=0⇒y=1
Do đó Q=x2+y2=(-1)2+12=2
giúp mk bài này vs!!!!
mk cần gấp lắm!!!!!!!(please!!!!!)x2
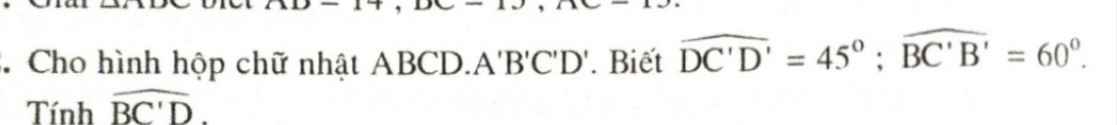
giúp mk bài này vs!!!!
mk cần gấp lắm!!!!!!!(please!!!!!)x2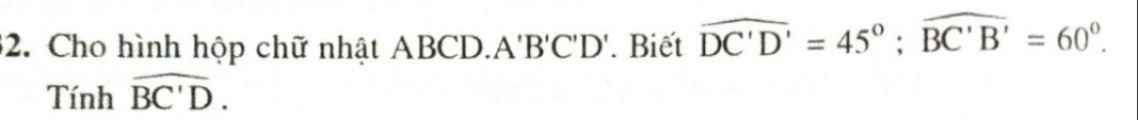
mk cần gấp mn giúp mk vs ạ
bình phương của 1 tổng , 1 hiệu
A) 49y2 - 42.x.y + 10x2 - 6x+9
B) 64x2 -48x - y2-20y - 91
C) x4+ 2x2 - y2-2y
D) x2 - 6x - y2-10y-16
A) \(...=\left(7y-3\right)^3\)
B) \(...=\left(4y-3\right)^3\)
C) \(...=x^4+2x^2+1-\left(y^2+2y+1\right)\)
\(=\left(x^2+1\right)^2-\left(y+1\right)^2\)
D) \(...=x^2-6x+9-\left(y^2-10y+25\right)\)
\(=\left(x-3\right)^2-\left(y-5\right)^2\)
cậu có thể giải chi tiết giúp tớ dc ko
Áp dụng \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
\(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
\(\left(a+b\right)^2=a^2+2ab+b^2;\left(a-b\right)^2=a^2-2ab+b^2\)
a, x15 =x
b, 1/x.(x+1)=1/30
c, (x2-7).(x2-25)=0
d, (x2-3).(x2-11)<0
e, (x2+4).(x2-49)<0
giải giúp mk vs
c: \(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\\x=-5\\x=5\end{matrix}\right.\)
4x2-9=0 mn giải hộ mk vs
ai bt làm câu này thì giúp mk vs mk đg cần gấp
( 1 + x/y + x2 / y2 ) . ( 1 - x/y ) . y3 / x3 - y3
Giúp mk bài này với ạ, mk đg cần gấp:
Tìm x:
(x + 4)(x+2) - x2 =7
\(\Leftrightarrow x^2+6x+8-x^2=7\\ \Leftrightarrow6x=-1\Leftrightarrow x=-\dfrac{1}{6}\)
(x + 4)(x+2) - x2 =7
x2+ 2x + 4x + 8 - x2 = 7
6x + 8 = 7
6x = 7 - 8 = -1
=> x = \(\dfrac{-1}{6}\)
ính gtln,gtnn
a =25x2-20x+7
b=-x2+2x-2
c=9x2-12x
d=3-10x2-4xy-4y2
e=4x-x2+1
giúp mk vs mk đg cần gấp
viết lại đề đi
\(A=25x^2-20x+7\)
\(\Leftrightarrow A=\left(5x-2\right)^2+3\ge3\)
Dấu " = " xảy ra \(\Leftrightarrow5x-2=0\Leftrightarrow x=\frac{2}{5}\)
Vậy \(minA=3\Leftrightarrow x=\frac{2}{5}\)
\(B=-x^2+2x-2\)
\(\Leftrightarrow B=-\left(x^2-2x+1\right)-3\)
\(\Leftrightarrow B=-\left(x-1\right)^2-3\le-3\)
Dấu " = " xảy ra \(\Leftrightarrow x=1\)
Vậy \(maxB=-3\Leftrightarrow x=1\)
\(C=9x^2-12x\)
\(\Leftrightarrow C=\left(9x^2-12x+4\right)-4\)
\(\Leftrightarrow C=\left(3x-2\right)^2-4\ge-4\)
Dấu " = " xảy ra \(\Leftrightarrow3x-2=0\Leftrightarrow x=\frac{2}{3}\)
Vậy \(minC=-4\Leftrightarrow x=\frac{2}{3}\)
\(D=3-10x^2-4xy-4y^2\)
\(\Leftrightarrow D=-\left(4y^2+4xy+x^2+9x^2\right)-3\)
\(\Leftrightarrow D=-\left[\left(2y-x\right)^2+3x^2\right]-3\le-3\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}2y-x=0\\3x^2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}y=0\\x=0\end{cases}}\)
Vậy \(maxD=-3\Leftrightarrow x=y=0\)
\(E=4x-x^2+1\)
\(\Leftrightarrow E=-\left(x^2-4x+4\right)+5\)
\(\Leftrightarrow E=-\left(x-2\right)^2+5\le5\)
Dấu " = " xảy ra \(\Leftrightarrow x=2\)
Vậy \(maxE=5\Leftrightarrow x=2\)
Tìm GTNN của C = x2 + \(\dfrac{4}{x}\) và D = x + \(\dfrac{4}{x^2}\)
giúp mk vs