Giải phương trình sinx - sin3x = cos2x
Giải phương trình sinx + sin2x + sin3x= cosx + cos2x+ cos3x
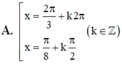
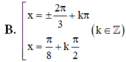
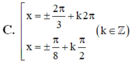
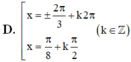
Chọn D
Ta sẽ biến đổi phương trình thành dạng tích
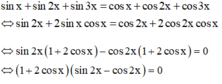
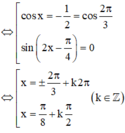
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm
Giải phương trình 5 ( sin x + sin 3 x + c o s 3 x 1 + 2 sin 2 x ) = cos 2 x + 3
![]()
![]()
![]()
![]()
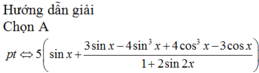
=cos2x+3

=cos2x+3 (*)
Ta có: 3( sin x – cosx) – 4 ( sin3x - cos3x)
= 3(sinx – cosx) – 4(sinx – cosx ).(sin2x + sinx. cosx+ cos2 x)
= 3( sin x – cosx) – 4(sinx – cosx).(1+ sinx. cosx)
= (sin x – cosx) . ( 3- 4 – 4sinx. cosx)
= ( sinx – cosx). (- 1- 4sinx. cosx) = - ( sinx – cosx)( 1+ 2sin2x)
Khi đó (*) trở thành
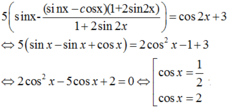
![]()
Phương trình sin 3 x + cos 2 x – sin x = 0 có tập nghiệm (0; π) là:
A. {π/4;3π/4}
B. {π/4}
C. {3π/4}
D. {π/6;π/4;3π/4}
Chọn A
Ta có sin3x+ cos2x- sinx= 0 ⇔ cos2x(2sinx+1)=0. Lưu ý trong khoảng (0;π), sinx > 0
Tìm nghiệm x của phương trình
2 ( sin 3 x + sin 2 x - sin x + 1 ) = 3 - 2 sin x - cos 2 x
thỏa mãn điều kiện sin x < 1 2
A. x = kπ ; k ∈ ℤ
B. x = π 2 + k π ; k ∈ ℤ
C. x = π 6 + k π ; k ∈ ℤ
D. x ∈ ∅
Phương trình đã cho tương đương với
2 sin 3 x + sin 2 x = 0 ⇔ sin x = 0 sin x = - 1 2
Do điều kiện
sin
x
<
1
2
nên sinx = 0 nên
x
=
kπ
;
k
∈
ℤ
Đáp án A
Giải phương trình
1, cos2x + cos6x + cos3x + cos5x = 0
2, sinx + sin2x + sin3x = 0
3, sinx + sin2x + sin3x + sin4x = 0
\( 2)\sin x + \sin 2x + \sin 3x = 0\\ \Leftrightarrow 2\sin 2x.\cos x + \sin 2x = 0\\ \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin 2x = 0\\ 2\cos x + 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} 2x = k\pi \\ \cos x = \dfrac{{ - 1}}{2} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{k\pi }}{2}\\ x = \pm \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z} } \right) \)
\( 3)\sin x + \sin 2x + \sin 3x + \sin 4x = 0\\ \Leftrightarrow \left( {\sin x + \sin 4x} \right) + \left( {\sin 2x + \sin 3x} \right) = 0\\ \Leftrightarrow 2\sin \dfrac{{5x}}{2}.\cos \dfrac{{3x}}{2} + 2\sin \dfrac{{5x}}{2}.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.\left( {\cos \dfrac{{3x}}{2} + \cos \dfrac{x}{2}} \right) = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.2\cos x.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin \dfrac{{5x}}{2} = 0\\ 2\cos x = 0\\ \cos \dfrac{x}{2} = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{2k\pi }}{5}\\ x = \dfrac{\pi }{2} + k\pi \\ x = \pi + 2k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \)
Cho phương trình sau: sin3x-sinx+cos2x=1.Phương trình có họ nghiệm x = π α + k 2 π α ; k ∈ Z hỏi giá trị của α :
A.1
B.6
C.3
D.4
Cho phương trình sau: sin3x-sinx+cos2x=1. Phương trình có họ nghiệm x = π a + k 2 π 3 , k ∈ Z hỏi giá trị của a.
A.1
B.6
C.3
D.4
Giải: (sin2x-cos2x)sinx+sin3x=(sinx+cosx)cosx
Giải: (sin2x-cos2x)sinx+sin3x=(sinx+cosx)cosx
\(\Leftrightarrow sin2x\cdot sinx-cos2x\cdot sinx+sin2x\cdot cosx+sinx\cdot cos2x=cosx\left(sinx+cosx\right)\)
=>\(sin2x\left(sinx+cosx\right)=cosx\left(sinx+cosx\right)\)
=>\(\left(sinx+cosx\right)\cdot\left(sin2x-cosx\right)=0\)
=>\(cosx\cdot\left(2sinx-1\right)\cdot\sqrt{2}\cdot sin\left(x+\dfrac{pi}{4}\right)=0\)
=>\(\left[{}\begin{matrix}cosx=0\\2sinx-1=0\\sin\left(x+\dfrac{pi}{4}\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{pi}{2}+kpi\\sinx=\dfrac{1}{2}\\x+\dfrac{pi}{4}=kpi\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{pi}{2}+kpi\\x=-\dfrac{pi}{4}+kpi\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{pi}{2}+kpi\\x=-\dfrac{pi}{4}+kpi\\x=\dfrac{pi}{6}+k2pi\\x=\dfrac{5}{6}pi+k2pi\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{pi}{2}+kpi;-\dfrac{pi}{4}+kpi;\dfrac{pi}{6}+k2pi;\dfrac{5}{6}pi+k2pi\right\}\)