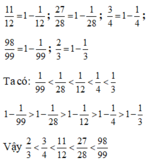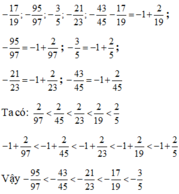Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần(giải thích vì sao): Sin78 độ ; có24độ35’ ; sin40độ ; cos87độ20’ ; sin42độ .
AQ
Những câu hỏi liên quan
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần(giải thích vì sao): Sin78 độ ; có24độ35’ ; sin40độ ; cos87độ20’ ; sin42độ .
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần(giải thích vì sao): Sin78 độ ; có24độ35’ ; sin40độ ; cos87độ20’ ; sin42độ .
\(\cos87^020'=\sin2^040'< \sin40^0< \sin42^0< \sin65^025'=\cos24^035'< \sin78^0\)
Đúng 2
Bình luận (0)
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a
)
sin
78
°
,
cos
14
°
,
sin
47
°
,
cos...
Đọc tiếp
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a ) sin 78 ° , cos 14 ° , sin 47 ° , cos 87 ° b ) tg 73 ° , cotg 25 ° , tg 62 ° , cotg 38 °
(Gợi ý: Bài này có 2 cách làm. Cách 1 là sử dụng máy tính. Cách 2 là sử dụng tính chất lượng giác của hai góc phụ nhau để đưa về cùng một tỉ số lượng giác rồi so sánh. Cách 2 nhanh hơn.)
a) Ta có:
sin 78 ° = cos 12 ° ; sin 47 ° = cos 43 ° V ì 12 ° < 14 ° < 43 ° < 87 ° n ê n cos 12 ° > cos 14 ° > cos 43 ° > cos 87 ° S u y r a : cos 87 ° < sin 47 ° < cos 14 ° < sin 78 ° b ) T a c ó : c o t g 25 ° = t g 65 ° ; c o t g 38 ° = t g 52 ° . V ậ y : c o t g 38 ° < t g 62 ° < c o t g 25 ° < t g 73 °
Đúng 0
Bình luận (0)
Sắp xếp các phân số sau theo thứ tự tăng dần và giải thích vì sao: 11 12 ; 27 28 ; 3 4 ; 98 99 ; 2 3
Sắp xếp các phân số sau theo thứ tự tăng dần và giải thích vì sao: − 17 19 ; − 95 97 ; − 3 5 ; − 21 23 ; − 43 45
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần :
a) \(\sin78^0,\cos14^0,\sin47^0,\cos87^0\)
b) \(tg73^0,cotg25^0,tg62^0,cotg38^0\)
a) cos14∘=sin76∘;cos87∘=sin3∘.cos14∘=sin76∘;cos87∘=sin3∘..
Vì sin3∘<sin47∘<sin76∘<sin78∘sin3∘<sin47∘<sin76∘<sin78∘ nên
cos78∘<cos76∘<cos47∘<cos3∘cos78∘<cos76∘<cos47∘<cos3∘.
b) cotg25∘=tg65∘;cotg38∘=tg52∘cotg25∘=tg65∘;cotg38∘=tg52∘.
Vì tg52∘<tg62∘<tg65∘<tg73∘tg52∘<tg62∘<tg65∘<tg73∘;
nên cotg38∘<tg62∘<cotg25∘<tg73∘cotg38∘<tg62∘<cotg25∘<tg73∘.
Nhận xét: Để so sánh các tỉ số lượng giác sin và côsin của các góc, ta đưa về so sánh cùng một loại tỉ số lượng giác (ví dụ cùng là sin của các góc). Tương tự như vậy, để so sánh các tỉ số lượng giác tang và côtang của các góc, ta đưa về so sánh cùng một loại tỉ số lượng giác (ví dụ cùng là tang của các góc).
Đúng 0
Bình luận (0)
∘..
∘ nên
∘.
∘.
∘;
∘.
Nhận xét: Để so sánh các tỉ số lượng giác sin và côsin của các góc, ta đưa về so sánh cùng một loại tỉ số lượng giác (ví dụ cùng là sin của các góc). Tương tự như vậy, để so sánh các tỉ số lượng giác tang và côtang của các góc, ta đưa về so sánh cùng một loại tỉ số lượng giác (ví dụ cùng là tang của các góc).
Đúng 0
Bình luận (0)
1.5 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần (không dùng bảng và máy tính). a) sin780, cos140, sin470, cos870 b) tan730, cot250, tan620, cot380 1.6 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần (không dùng bảng và máy tính).a) tan420, tan560, cot30, cot180 b) sin130, cos470, tan460, cot20
Đọc tiếp
1.5 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần (không dùng bảng và máy tính).
a) sin780, cos140, sin470, cos870 b) tan730, cot250, tan620, cot380
1.6 Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần (không dùng bảng và máy tính).
a) tan420, tan560, cot30, cot180 b) sin130, cos470, tan460, cot20
Bài 1.6
a) \(\cos14^0=\sin76^0\)
\(\cos87^0=\sin3^0\)
Do đó: \(\cos87^0< \sin47^0< \cos14^0< \sin78^0\)
b) \(\cot25^0=\tan65^0\)
\(\cot38^0=\tan52^0\)
Do đó: \(\cot38^0< \tan62^0< \cot25^0< \tan73^0\)
Đúng 0
Bình luận (0)
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
tg73o, cotg25o, tg62o, cotg38o
Ta có: cotg25o = tg65o; cotg38o = tg52o.
Vậy: cotg38o < tg62o < cotg25o < tg73o
Đúng 0
Bình luận (0)
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
sin78o, cos14o, sin 47o, cos87o
Ta có: sin 78o = cos12o; sin 47o = cos 43o
Vì 12o < 14o < 43o < 87o
nên cos 12o > cos 14o > cos 43o > cos 87o
Suy ra: cos 87o < sin47o < cos14o < sin78o
Đúng 0
Bình luận (0)