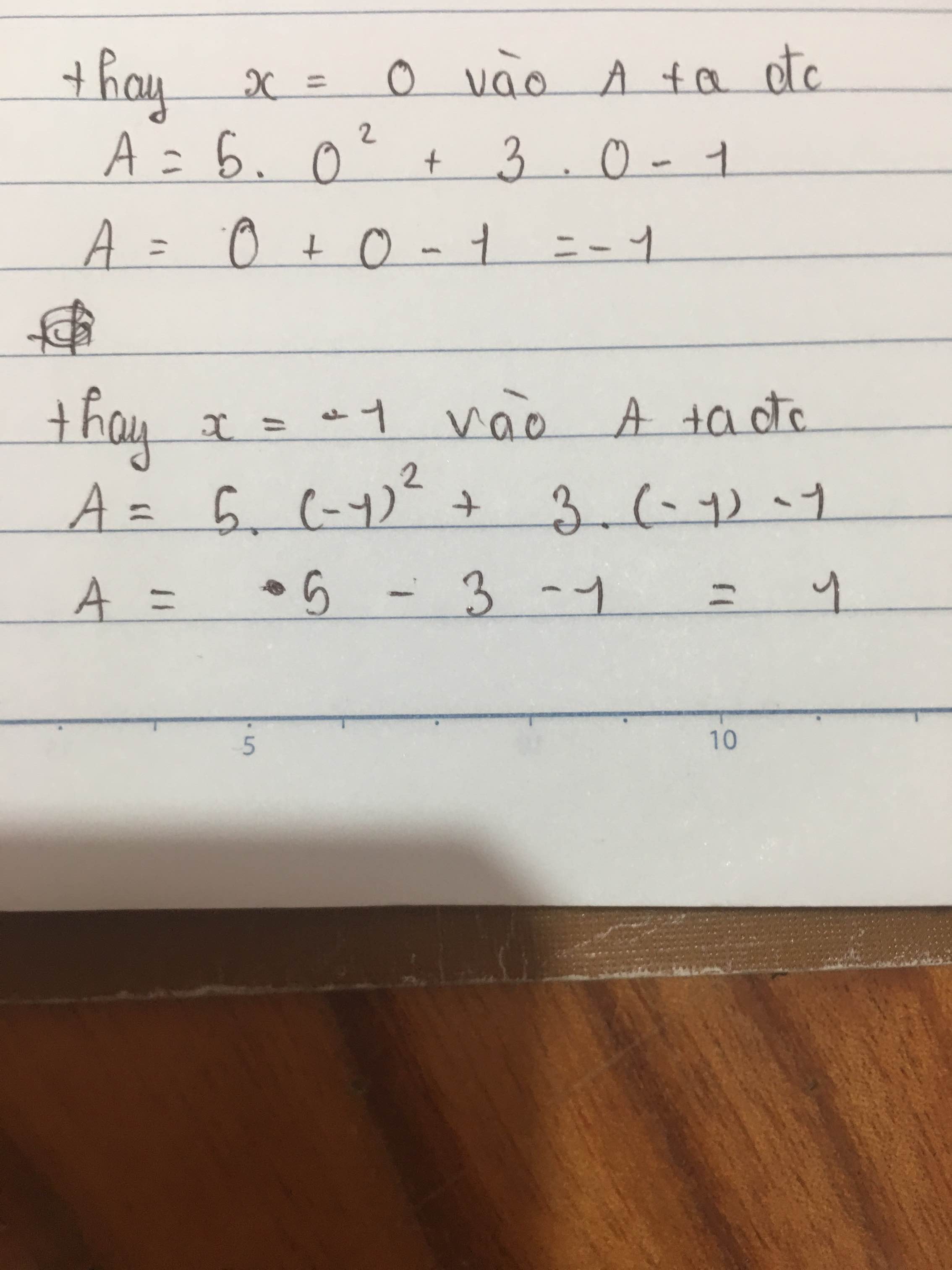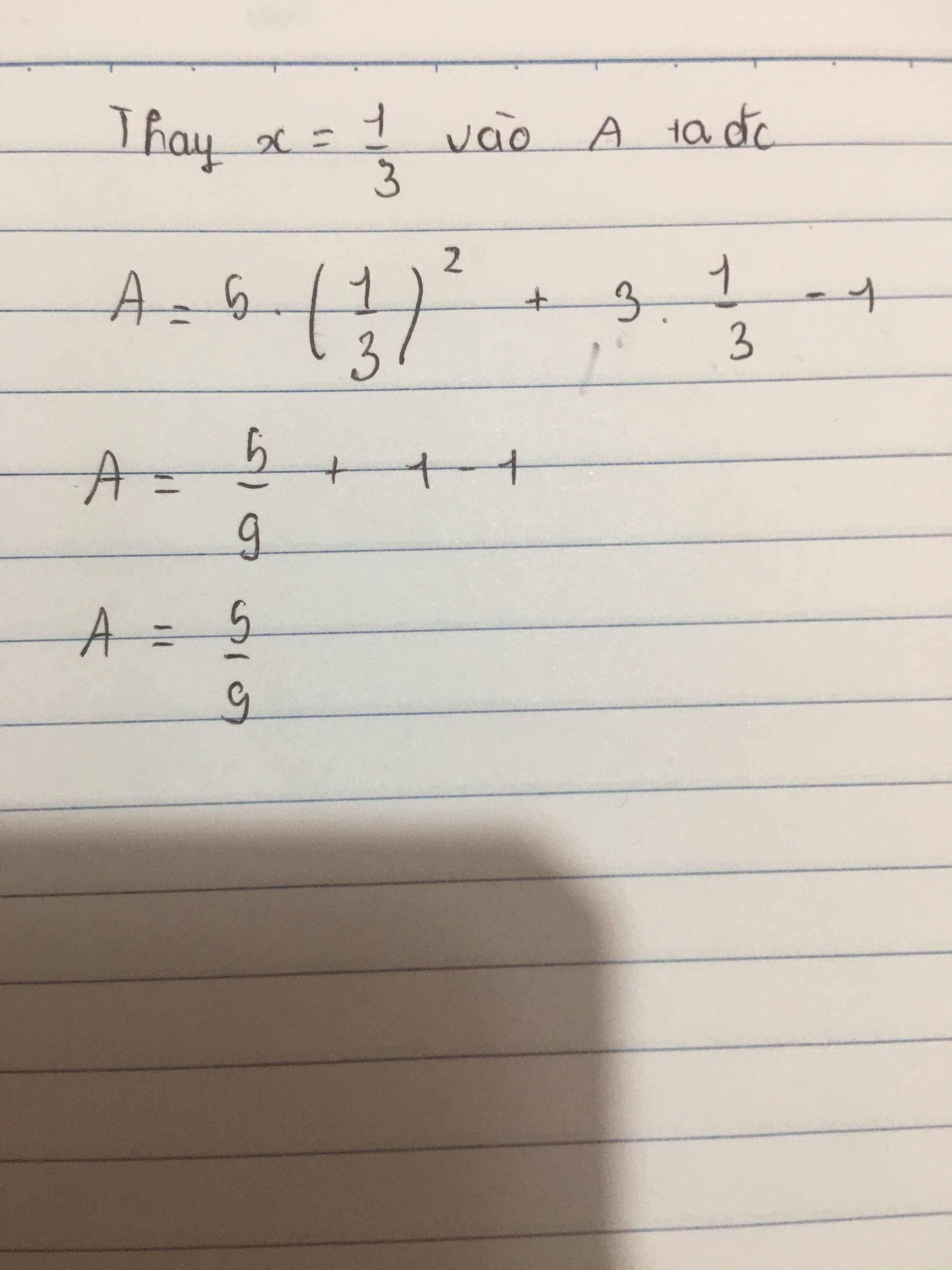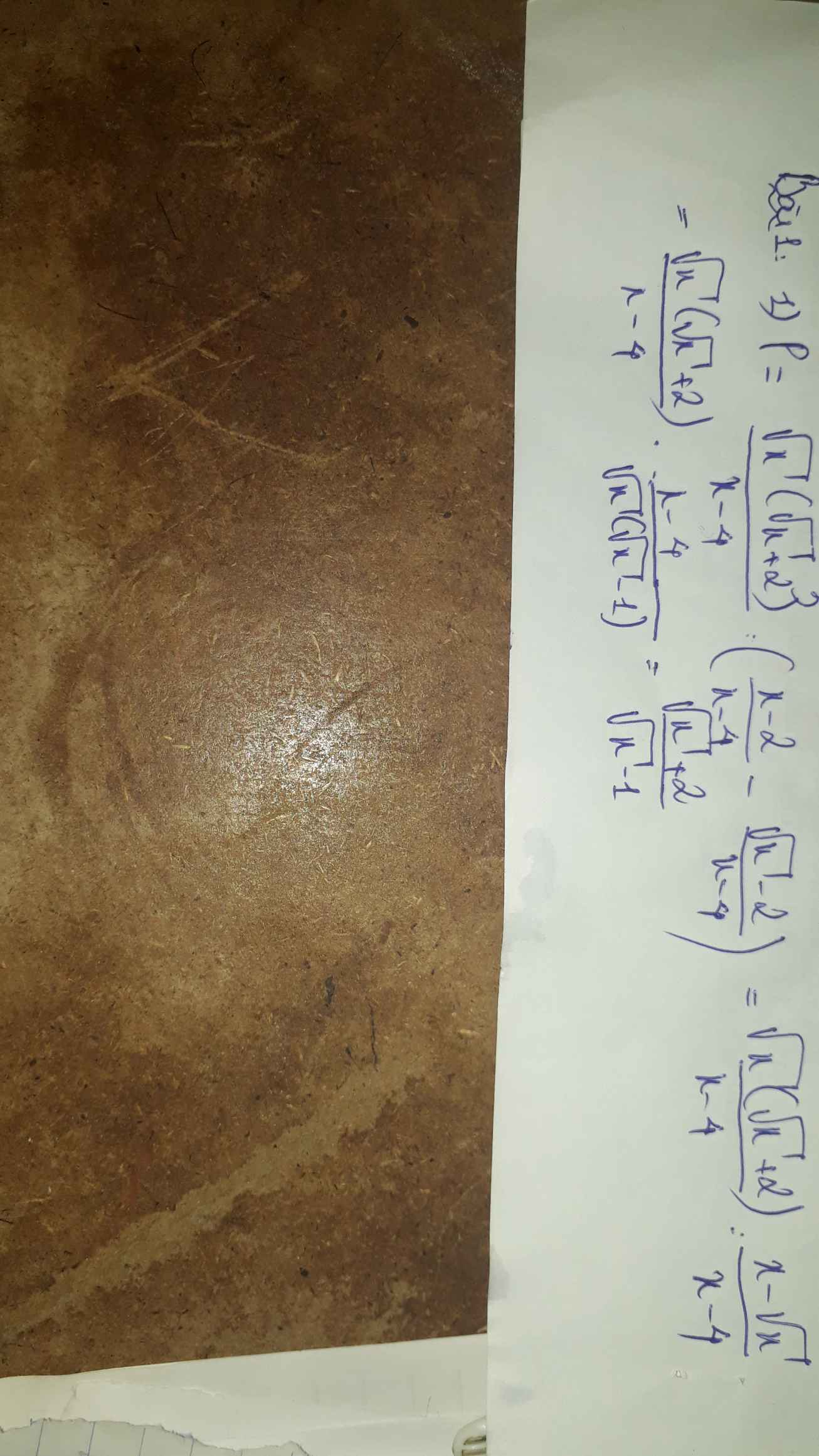Tính giá trị của biểu thức \(x^2+x+41\)tại x = 0;1;2;3...;39.Có nhận xét gì về các giá trị tìm được.
TN
Những câu hỏi liên quan
H24
SGK Toán 8 tập 1– Chân trời sáng tạo
22 tháng 7 2023 lúc 8:59
Cho biểu thức \(P = \dfrac{{{x^2} - 1}}{{2x + 1}}\)
a) Tính giá trị của biểu thức tại \(x = 0\)
b) Tại \(x = - \dfrac{1}{2}\), giá trị của biểu thức có xác định không? Tại sao?
`a, x = 0 <=> (0^2-1)/(2.0+1) = -1/1 = -1`
`b,` Biểu thức không xác định vì mẫu `= 0`
Đúng 1
Bình luận (0)
1 a. Rút gọn biểu thức sau A = \(\left(x^{\text{2}}-2x+4\right):\left(x^3+8\right)-x^2\) rồi tính giá trị của A tại x = -2
b. Rút gọn biểu thức B = (x - 2) : 2x + 5x rồi tính giá trị của biểu thức B tại x = 0
a) tính giá trị của biểu thức: x^2+2y tại x=2, y= –3 b) tính giá trị của biểu thức: x^2+2xy+y^2 tại x=4, y=6 c) tính giá trị của biểu thức: P= x^2-4xy+4y^2 tại x=1 và y= 1/2
a: Khi x=2 và y=-3 thì \(x^2+2y=2^2+2\cdot\left(-3\right)=4-6=-2\)
b: \(A=x^2+2xy+y^2=\left(x+y\right)^2\)
Khi x=4 và y=6 thì \(A=\left(4+6\right)^2=10^2=100\)
c: \(P=x^2-4xy+4y^2=\left(x-2y\right)^2\)
Khi x=1 và y=1/2 thì \(P=\left(1-2\cdot\dfrac{1}{2}\right)^2=\left(1-1\right)^2=0\)
Đúng 3
Bình luận (0)
1. a) Tìm điều kiện xác định của biểu thức A = \(\dfrac{\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}}{1+\dfrac{x+1}{x-2}}\)
b) tính giá trị của biểu thức A tại x=0
c) tính giá trị của x để A =0
\(a,ĐK:x\ne\pm1;x\ne2\\ b,A=\dfrac{\dfrac{0+1}{0-1}-\dfrac{0-1}{0+1}}{1+\dfrac{0+1}{0-2}}=\dfrac{-1+1}{1-\dfrac{1}{2}}=0\\ c,A=0\Leftrightarrow\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}=0\\ \Leftrightarrow\left(x+1\right)^2-\left(x-1\right)^2=0\\ \Leftrightarrow4x=0\Leftrightarrow x=0\left(tm\right)\)
Đúng 2
Bình luận (1)
Cho biểu thức \(A=5x^2+3x-1\).
Tính giá trị của biểu thức tại \(x=0\) ; \(x=-1\) ; \(x=\dfrac{1}{3}\)
Tại \(x=0\) ta có:
\(A=5.0^2+3.0-1=5.0+3.0-1=0+0-1=-1\)
Vậy tại \(x=0\) thì biểu thức A là -1
Tại \(x=-1\) ta có
\(A=5.\left(-1\right)^2+3.\left(-1\right)-1=5.1+3.\left(-1\right)-1=5-3-1=1\)
Vậy tại \(x=-1\) thì biểu thức A là 1
Tại \(x=\dfrac{1}{3}\) ta có
\(A=5.\left(\dfrac{1}{3}\right)^2+3.\dfrac{1}{3}-1=5.\dfrac{1}{9}+3.\dfrac{1}{3}-1=\dfrac{5}{9}+1-1=\dfrac{5}{9}\)
Vậy tại \(x=\dfrac{5}{9}\) thì biểu thức A là \(\dfrac{5}{9}\)
Đúng 0
Bình luận (0)
Bài 10: Cho biểu thức:A=x^2-1/x^2+3x+2
a, Tìm ĐKXĐ của x
b, Tính giá trị của phân thức tại x=2020
c, Tính giá trị của x để A=0
\(a,ĐK:x\ne-1;x\ne-2\\ b,A=\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x+2\right)}=\dfrac{x-1}{x+2}\\ x=2020\Leftrightarrow A=\dfrac{2019}{2022}=\dfrac{673}{674}\\ c,A=0\Leftrightarrow x-1=0\Leftrightarrow x=1\left(tm\right)\)
Đúng 1
Bình luận (0)
cho biểu thức P=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}:\left(\dfrac{x-2}{x-4}-\dfrac{1}{\sqrt{x}+2}\right)\) với x>0;x\(\ne\)1;x\(\ne\)4
1.rút gọn biểu thức P
2.tìm x thỏa mãn P>1
3.tính giá trị của P khi x=\(\dfrac{1}{4}\)
cho biểu thức P=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}:\left(\dfrac{x-2}{x-4}-\dfrac{1}{\sqrt{x}+2}\right)\) với x>0;x\(\ne\)1;x\(\ne\)4
1.rút gọn biểu thức P
2.tìm x thỏa mãn P>1
3.tính giá trị của P khi x=\(\dfrac{1}{4}\)
1 . Rút gọn biểu thức B = (x - 2) : 2x + 5x rồi tính giá trị của biểu thức B tại x = 0
\(ĐK:x\ne0\)
Vậy tại x=0 thì k có gt nào của B thỏa mãn
Đúng 1
Bình luận (0)