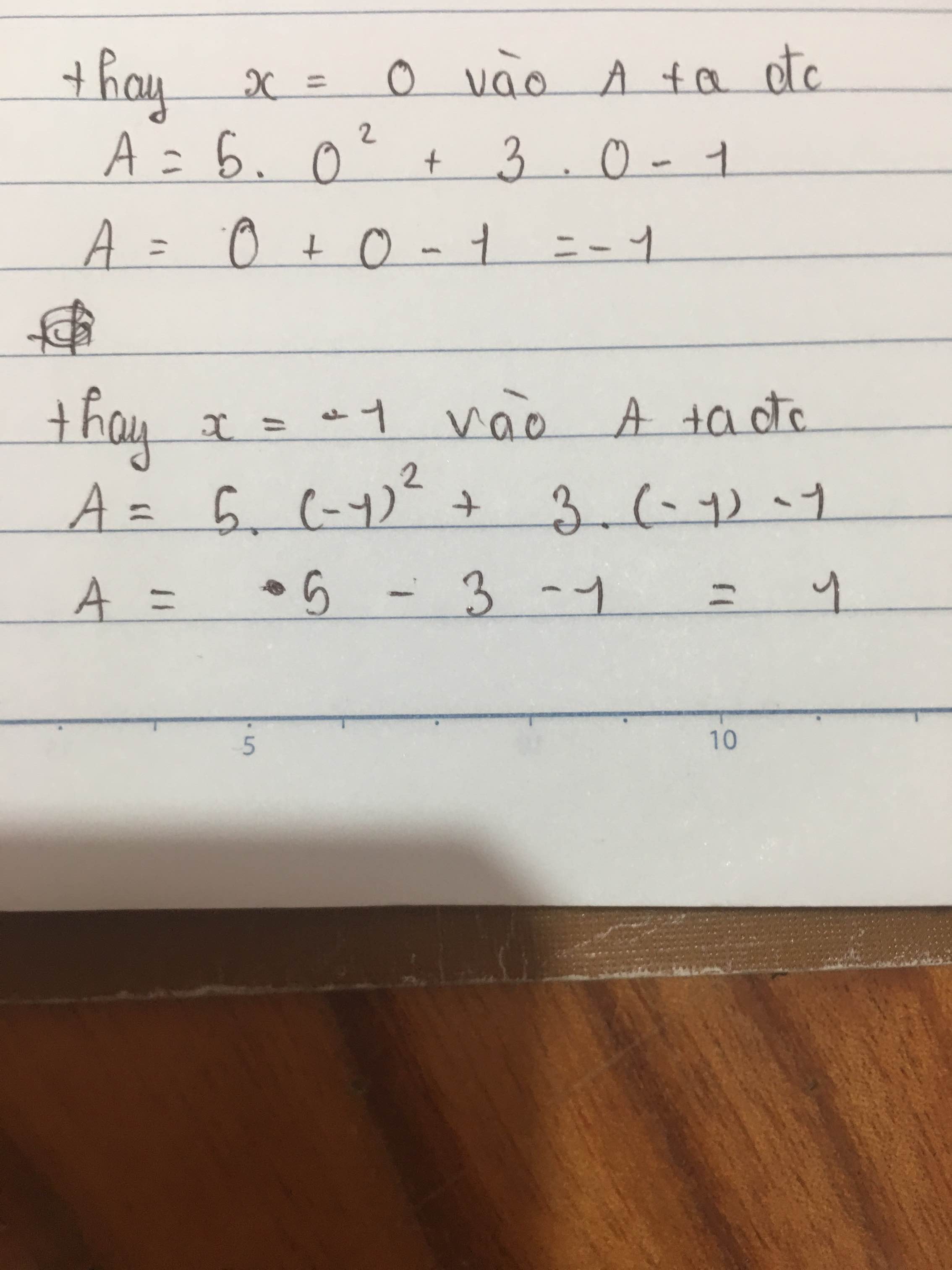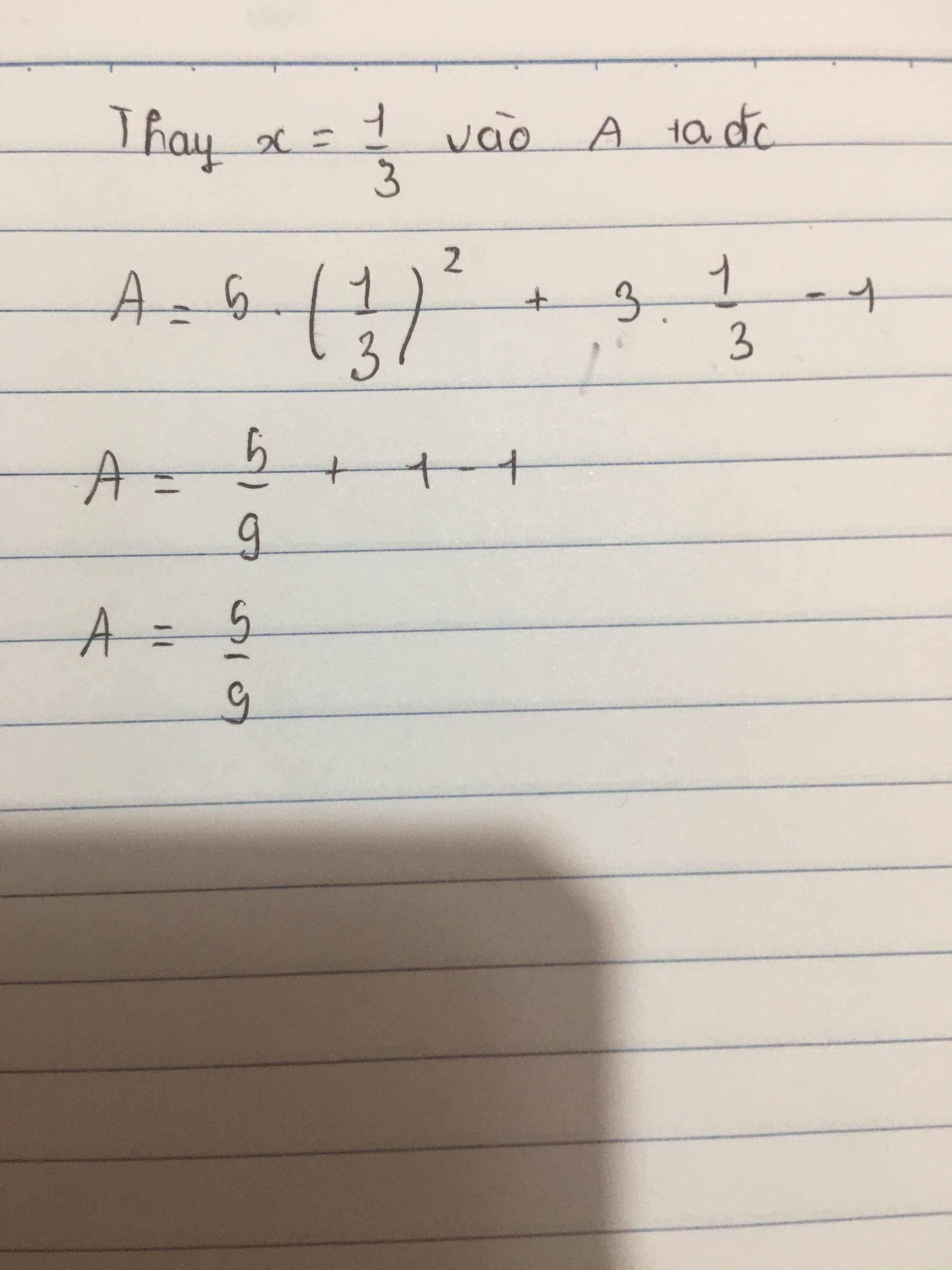Tại \(x=0\) ta có:
\(A=5.0^2+3.0-1=5.0+3.0-1=0+0-1=-1\)
Vậy tại \(x=0\) thì biểu thức A là -1
Tại \(x=-1\) ta có
\(A=5.\left(-1\right)^2+3.\left(-1\right)-1=5.1+3.\left(-1\right)-1=5-3-1=1\)
Vậy tại \(x=-1\) thì biểu thức A là 1
Tại \(x=\dfrac{1}{3}\) ta có
\(A=5.\left(\dfrac{1}{3}\right)^2+3.\dfrac{1}{3}-1=5.\dfrac{1}{9}+3.\dfrac{1}{3}-1=\dfrac{5}{9}+1-1=\dfrac{5}{9}\)
Vậy tại \(x=\dfrac{5}{9}\) thì biểu thức A là \(\dfrac{5}{9}\)