Tìm X để biểu thức sau có nghĩa:
a, Căn -5/x2+6
b, Căn 2/x2
c, Căn 1/-1+x
d, Căn 4/x+3
DT
Những câu hỏi liên quan
Tìm x để biểu thức sau có nghĩa:
a, căn x2-2x+1
b, căn x+3 + căn x+9
c, căn x-1/x+2
d, căn x-2 + 1/x-5
(phần này dấu căn chỉ đến x-2 thôi nhé)
\(a,\)\(\sqrt{x^2-2x+1}=\sqrt{\left(x-1\right)^2}\)
\(đkxđ\Leftrightarrow\sqrt{\left(x-1\right)^2}\ge0\)
\(\Rightarrow x-1\ge0\Rightarrow x\ge1\)
\(b,\)\(\sqrt{x+3}+\sqrt{x+9}\)
\(đkxđ\Leftrightarrow\hept{\begin{cases}x+3\ge0\\x+9\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ge-3\\x\ge-9\end{cases}}}\)
\(\Rightarrow x\ge-3\)
Đúng 0
Bình luận (0)
\(c,\)\(\sqrt{\frac{x-1}{x+2}}\)
\(đkxđ\Leftrightarrow\hept{\begin{cases}x+2\ne0\\\frac{x-1}{x+2}\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ne-2\\\frac{x-1}{x+2}\ge0\end{cases}}}\)
\(\frac{x-1}{x+2}\ge0\)\(\Rightarrow\orbr{\begin{cases}x-1\ge0;x+2>0\\x-1\le0;x+2< 0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x\ge-1;x>-2\\x\le1;x< 2\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x\ge-1\\x< 2\end{cases}}\)
Vậy căn thức xác định khi x \(\ge\)-1 hoawck x < 2
Đúng 0
Bình luận (0)
\(d,\)\(\sqrt{x-2}-\frac{1}{x-5}\)
\(đkxđ\Leftrightarrow\orbr{\begin{cases}\sqrt{x-2}xđ\\\frac{1}{x-5}xđ\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x-2\ge0\\x-5\ne0\end{cases}\Rightarrow\orbr{\begin{cases}x\ge2\\x\ne5\end{cases}}}\)
Vậy biểu thức xác định \(\Leftrightarrow x\ge2\)và \(x\ne5\)
Đúng 0
Bình luận (0)
Tìm x để các căn thức sau có nghĩa:
a,\(\sqrt{\dfrac{2x-3}{2x^2+1}}\)
b,\(\sqrt{\dfrac{3}{1-5x}}\)
a. ĐKXĐ: Mọi x
b. ĐKXĐ: x > \(\dfrac{1}{5}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm điều kiện để căn thức sau có nghĩa:
a) \(\sqrt{2x-5}\) b)\(\sqrt{\dfrac{-1}{3x-2019}}\) c)\(\dfrac{\sqrt{x+1}}{\sqrt{x-3}}\)
a: ĐKXĐ: \(x\ge\dfrac{5}{2}\)
b: ĐKXĐ: \(x< 673\)
c: ĐKXĐ: x>3
Đúng 1
Bình luận (1)
Bài 1: Tìm điều kiện của x để các biểu thức sau có nghĩa.
a) Căn(x-2) + 1/căn(x-3)
b) Căn (x+3/x-2)
Bài 2: Thức hiện phép tính.
a) A= Căn(2- căn 5)2 - căn 5
b) B= Căn (7- 4căn3) + căn 3
c) C= Căn (5 - 2căn6) + Căn (5 + 2căn6)
d) D= (căn 2 + căn 10) / (1 + căn 5)
e) E= Căn(2 - căn 3) + Căn(2 + căn3)
Tìm x để mỗi căn thức sau có nghĩa:
a
)
2
x
+
7
b
)
-
3
x
+
4
c
)
1
-
1
+
x
d
)
1
+
x
2
Đọc tiếp
Tìm x để mỗi căn thức sau có nghĩa:
a ) 2 x + 7 b ) - 3 x + 4 c ) 1 - 1 + x d ) 1 + x 2
a)Ta có 2 x + 7 có nghĩa khi 2 x + 7 ≥ 0
2 x + 7 ≥ 0 ⇔ 2 x ≥ - 7 ⇔ x ≥ - 7 2
b ) - 3 x + 4 có nghĩa khi - 3 x + 4 ≥ 0
- 3 x + 4 ≥ 0 ⇔ - 3 x ≥ - 4 ⇒ x ⩽ 4 3
Đúng 0
Bình luận (0)
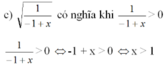
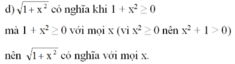
Tìm x để các biểu thức sau có nghĩa e, căn 2x-5 f, căn -3+6 g, căn x+4 trên -5 h, căn 7 trên 4-2x
e: ĐKXĐ: \(x\ge\dfrac{5}{2}\)
g: ĐKXĐ: \(x\le-4\)
Đúng 0
Bình luận (0)
Bài 1. Tìm điệu kiện của x để biểu thức A= căn 5+4x +căn 7-3x có nghĩa
Bài 2 Tìm x thỏa mãn:
a) căn 4x-4 +căn 9x-9- căn 25x-25 =7
b)căn 2x^2-3 =4 rất mong mọi người giúp đỡ ạ
\(2,\\ a,\sqrt{4x-4}+\sqrt{9x-9}-\sqrt{25x-25}=7\left(x\ge1\right)\\ \Leftrightarrow2\sqrt{x-1}+3\sqrt{x-1}-5\sqrt{x-1}=7\\ \Leftrightarrow0\sqrt{x-1}=7\Leftrightarrow x\in\varnothing\\ b,\sqrt{2x^2-3}=4\left(x\le-\dfrac{\sqrt{6}}{2};\dfrac{\sqrt{6}}{2}\le x\right)\\ \Leftrightarrow2x^2-3=16\\ \Leftrightarrow x^2=\dfrac{19}{2}\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{19}{2}}\left(tm\right)\\x=-\sqrt{\dfrac{19}{2}}\left(tm\right)\end{matrix}\right.\)
Đúng 5
Bình luận (0)
\(1,\\ A=\sqrt{5+4x}+\sqrt{7-3x}\\ ĐKXĐ:\left\{{}\begin{matrix}5+4x\ge0\\7-3x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{5}{4}\\x\le\dfrac{7}{3}\end{matrix}\right.\)
Đúng 4
Bình luận (1)
Bài 2:
a) \(\sqrt{4x-4}+\sqrt{9x-9}-\sqrt{25x-25}=7\left(đk:x\ge1\right)\)
\(\Leftrightarrow2\sqrt{x-1}+3\sqrt{x-2}-5\sqrt{x-1}=7\)
\(\Leftrightarrow0=7\left(VLý\right)\)
Vậy \(S=\varnothing\)
b) \(\sqrt{2x^2-3}=4\left(đk:-\sqrt{\dfrac{3}{2}}\ge x\ge\sqrt{\dfrac{3}{2}}\right)\)
\(\Leftrightarrow2x^2-3=16\)
\(\Leftrightarrow2x^2=19\Leftrightarrow x^2=\dfrac{19}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{19}{2}}\left(tm\right)\\x=-\sqrt{\dfrac{19}{2}}\left(tm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm x để biểu thức sau có nghĩa:
a, căn x+3 + căn x2+9
b, căn x-1/x+2
c, căn x-2 + 1/x-5
( phần này căn chỉ đến x-2 thôi nhé)
a) \(\sqrt{x+3}+\sqrt{x^2+9}\)
Ta thấy \(x^2\ge0\Rightarrow x^2+9\ge9\Rightarrow\sqrt{x^2+9}\ge3\)(luôn xác định)
Vậy để biểu thức xác định thì \(\sqrt{x+3}\)phải xác định
\(\Rightarrow x+3\ge0\Leftrightarrow x\ge-3\)
Vậy \(ĐKXĐ:x\ge-3\)
Đúng 0
Bình luận (0)
b) \(\sqrt{\frac{x-1}{x+2}}\)
Để biểu thức trên xác định thì x - 1 và x + 2 cùng dấu
\(TH1:\hept{\begin{cases}x-1>0\\x+2>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x>1\\x>-2\end{cases}}\Rightarrow x>1\)
\(TH1:\hept{\begin{cases}x-1< 0\\x+2< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 1\\x< -2\end{cases}}\Rightarrow x< -2\)
Vậy \(ĐKXĐ:x>1;x< -2\)
Đúng 0
Bình luận (0)
c) \(\sqrt{x-1}+\frac{1}{x-5}\)
Để biểu thức xác định thì \(x-5\ne0\Leftrightarrow x\ne5\)
Và \(x-1\ge0\Leftrightarrow x\ge1\)
Vậy \(ĐKXĐ:x\ge1;x\ne5\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm điều kiện xác định để các biểu thức sau có nghĩa;
a,1/1-căn x^2-3
b,x-1/2-căn 3x+1
c,2/căn x^2-x+1
d,1/căn x- căn 2x-1