tìm min max của y = sin x trên đoạn \(\left[\frac{-\pi}{3};\frac{2\pi}{3}\right]\)
Cách lập bảng biến thiên để tìm min max ntn, chỉ rõ cách lập bảng biến thiên giúp mh đk k, cảm ơn nhé!
LM
Những câu hỏi liên quan
Tìm giá trị max, min của các hàm số sau:
1, y= 2 - \(\sin\left(\dfrac{3\pi}{2}+x\right)\cos\left(\dfrac{\pi}{2}+x\right)\)
2, y= \(\sqrt{5-2\sin^2x.\cos^2x}\)
1, \(y=2-sin\left(\dfrac{3x}{2}+x\right).cos\left(x+\dfrac{\pi}{2}\right)\)
\(y=2-\left(-cosx\right).\left(-sinx\right)\)
y = 2 - sinx.cosx
y = \(2-\dfrac{1}{2}sin2x\)
Max = 2 + \(\dfrac{1}{2}\) = 2,5
Min = \(2-\dfrac{1}{2}\) = 1,5
2, y = \(\sqrt{5-\dfrac{1}{2}sin^22x}\)
Min = \(\sqrt{5-\dfrac{1}{2}}=\dfrac{3\sqrt{2}}{2}\)
Max = \(\sqrt{5}\)
Đúng 2
Bình luận (0)
Tìm Max, Min của hàm số:1) ydfrac{x+1+sqrt{x-1}}{x+1+2sqrt{x-1}}2) ysin^{2016}x+cos^{2016}x 3) y2cos x-dfrac{4}{3}cos^3x trên left[0;dfrac{pi}{2}right]4) ysin2x-sqrt{2}x+1,xinleft[0;dfrac{pi}{2}right]5) ydfrac{4-cos^2x}{sqrt{sin^4x+1}},xinleft[-dfrac{pi}{3};dfrac{pi}{3}right]
Đọc tiếp
Tìm Max, Min của hàm số:
1) \(y=\dfrac{x+1+\sqrt{x-1}}{x+1+2\sqrt{x-1}}\)
2) \(y=\sin^{2016}x+\cos^{2016}x\)
3) \(y=2\cos x-\dfrac{4}{3}\cos^3x\) trên \(\left[0;\dfrac{\pi}{2}\right]\)
4) \(y=\sin2x-\sqrt{2}x+1,x\in\left[0;\dfrac{\pi}{2}\right]\)
5) \(y=\dfrac{4-cos^2x}{\sqrt{sin^4x+1}},x\in\left[-\dfrac{\pi}{3};\dfrac{\pi}{3}\right]\)
Tìm max min của y=sin(x+pi/3)-sinx
\(y=sin\left(x+\dfrac{\pi}{3}\right)-sinx\)
\(=\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx-sinx\)
\(=\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\)
\(=cos\left(x+\dfrac{\pi}{6}\right)\in\left[-1;1\right]\)
\(\Rightarrow\left\{{}\begin{matrix}y_{mịn}=-1\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\\y_{max}=1\Leftrightarrow x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
tìm min max của phương trình y=sin^2x-2sinx-3 trên khoảng [pi/4;2pi/3]
Xem chi tiết
bạn nên dùng hàm fx để ghi dễ nhìn hơn
Đúng 0
Bình luận (0)
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
a) \(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\)
b) \(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\)
a) Vẽ đồ thị:
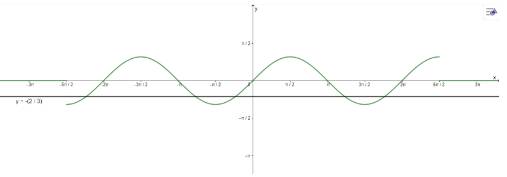
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
Đúng 0
Bình luận (0)
Tìm min, max của hàm số: y= \(\frac{\pi}{4}\)+ sin2x
Tìm Min, Max của : y =\(\dfrac{4}{\sqrt{2-cos\left(x-\dfrac{\pi}{6}\right)}+3}\)
ĐK: Biểu thức xác định với mọi `x`.
`y_(min) <=> (\sqrt(2-cos(x-π/6))+3)_(max) <=> (cos(x-π/6))_(max)`
`<=> cos(x-π/6)=1 <=> x-π/6=k2π <=> x = π/6+k2π ( k \in ZZ)`.
`=> y_(min) = 1`
`y_(max) <=> (\sqrt(2-cos(x-π/6))+3)_(min) <=> (cos(x-π/6))_(min)`
`<=> cos(x-π/6)=-1 <=> x -π/6= π+k2π <=> x = (7π)/6+k2π (k \in ZZ)`
`=> y_(max) = (6-2\sqrt3)/3`.
Đúng 0
Bình luận (1)
Tìm Min của: \(y=1+\sqrt{3}sin^2x\left(x-\frac{\pi}{3}\right)\)
Chắc đề là \(y=1+\sqrt{3}sin^2\left(x-\frac{\pi}{3}\right)\)
Do \(sin^2\left(x-\frac{\pi}{3}\right)\ge0;\forall x\Rightarrow y\ge1\)
\(y_{min}=1\) khi \(sin\left(x-\frac{\pi}{3}\right)=0\)
\(\Leftrightarrow x-\frac{\pi}{3}=k\pi\Rightarrow x=\frac{\pi}{3}+k\pi\)
Đúng 0
Bình luận (0)
Số nghiệm của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) trên đoạn \(\left[ {0;\pi } \right]\) là:
A.4
B.1
C.2
D.3
Ta có
\(\begin{array}{l}\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\frac{\pi }{4} + k2\pi ;k \in Z\\x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\pi {\rm{ - }}\frac{\pi }{4} + k2\pi ;k \in Z\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = {\rm{ }}k2\pi ;k \in Z\\x{\rm{ }} = {\rm{ }}\frac{\pi }{2} + k2\pi ;k \in Z\end{array} \right.\end{array}\)
Mà \(x \in \left[ {0;\pi } \right]\) nên \(x \in \left\{ {0;\frac{\pi }{2}} \right\}\)
Vậy phương trình đã cho có số nghiệm là 2.
Chọn C
Đúng 0
Bình luận (0)