Tìm a sao cho đa thức \(x^3+ax^2+5x+3\) chia hết cho đa thức \(x^2+2x+3\)
HD
Những câu hỏi liên quan
Bài 2: Tìm a,b để :
a. Đa thức 3x^3 + 2x2 -7x + a chia hết cho đa thức 3x-1b. ax^2 + 5x^4 chia hết cho (x-1)^2c. Đa thức 2x^2 + ã +1 chia x-3 được d là 4d. 2x^3 - x^2 + ax + b chia hết cho x^2 -1Hộ aka: 3x^3+2x^2-7x+a chia hêt cho 3x-1
=>3x^3-x^2+3x^2-x-6x+2+a-2 chia hết cho 3x-1
=>a-2=0
=>a=2
c: =>2x^2-6x+(a+6)x-3a-18+3a+19 chia x-3 dư 4
=>3a+19=4
=>3a=-15
=>a=-5
d: 2x^3-x^2+ax+b chiahêt cho x^2-1
=>2x^3-2x-x^2+1+(a+2)x+b-1 chia hết cho x^2-1
=>a+2=0 và b-1=0
=>a=-2 và b=1
Đúng 0
Bình luận (0)
giúp mình với:
tìm hệ số a sao cho đa thức: 2x2-ax+5 chia cho đa thức 2x-3 có số dư bằng 2
tìm hệ số a và b sao cho đa thức: ax3+bx-24 chia hết cho (x+1)(x+3)
a) 2x-3=0 <=> x=\(\dfrac{3}{2}\) để \(\left(2x^2-ax+5\right):\left(2x-3\right)\) thì \(2x^2-ax+5=2\)
Thay x= \(\dfrac{3}{2}\) vào \(2x^2-ax+5\), ta được:
\(\dfrac{9}{2}-\dfrac{3}{2}a+5=2\)
<=> \(-\dfrac{3}{2}a=2-5-\dfrac{9}{2}\) <=>a=5
Đúng 0
Bình luận (0)
lười quá ~~
bài 1
vì đa thức bị chia bậc 2, đa thức chia bậc nhất
=> đa thức thương sẽ có dạng bx+c
theo đề ta có
\(2x^2-ax+5=\left(bx+c\right)\left(2x-3\right)+2\\ < =>2x^2-ax+5=2bx^2-3bx+2cx-3c+2\\ < =>2x^2-ax+5=2bx^2-x\left(2c-3b\right)-3c+2\\ < =>\left\{{}\begin{matrix}2x^2=2bx^2\\ax=x\left(2c-3b\right)\\5=2-3c\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}b=1\\c=-1\\a=2c-3b\end{matrix}\right.\\ =>a=2\left(-1\right)-3.1\\ =>a=-5\)
vậy a = -5
bài 2 ko hiểu sao mình ko làm được, chắc sai ở đâu đợi mình làm lại nhé
Đúng 0
Bình luận (9)
Tìm a để đa thức 2x3 + 5x - 2x + a chia hết cho đa thức 2x2 -x + 1
Xác định các số a và b sao cho x3 + ax2 + 2x + b chia hết cho x2 + x +1.
phân tích đa thức sau thành nhân tử : 81x4 + 1
Tìm a,b sao cho:
a,Đa thức x^4-x^3+6x^2-x+a chia hết cho x^2-x+5
b,Đa thức 2x^3-3x^2+x+a chia hết cho x+2
c,Đa thức 3x^3+ax^2+bx+9 chia hết cho x+3 và x-3
Cau a va b dat cot tim so du .Vi la phep chia het nen du bang 0.Cau c thi da thuc se chia het cho tich (x+3)(x-3) lam tuong tu hai cau a va b
Đúng 0
Bình luận (2)
tìm a để
a) đa thức 3x^3+2x^2-7x+a chia hết cho đa thức 3x-1
b) đa thức x^3+3x^2+5x+a sao chia hết cho x+3
Để : \(3x^3+2x^2-7x+a⋮3x-1\)<=> \(a-2=0\)
<=> \(a=2\)
Vậy a = 2
Để \(x^3+3x^2+5x+a⋮x+3\)<=> \(a-66=0\)
<=> \(a=66\)
Vậy a = 66
1) Cho đa thức A= x^4 - 2x^3 + 3x^2 - 5x + 10 và B= x^2 - x + 1. Tìm các đa thức Q và R sao cho A = BQ+R
2) Xác địng số dư khi chia đa thức f(x)= x^25 + x^20 + x^15 + x^30 + x^5 +1 cho
a. x-1
b. x+1
c. x^2-1
3) Tìm x nguyên sao cho giá trị biểu thức x^3 - 2x^2 + 2x chia hết cho x^2 - x +1
4) Xác định số a để
a.x^4 + ax^2 + 1 chia hết cho x^2 - 2x+1
b.2x^2 + ax + 5 chia x + 3 dư 41
Tìm a sao cho đa thức \(x^3+ax^2+5x+3\) chia hết cho x2+2x+3
Giả sử P(x) là thương của phép chia \(x^3+ax^2+5x+3\) cho \(x^2+2x+3\).
Khi đó: \(x^3+ax^2+5x+3=\left(x^2+2x+3\right).P\left(x\right)\)
NX: P(x) là biểu thức bậc nhất. có dạng \(bx+c\) .
Nên \(x^3+ax^2+5x+3=\left(x^2+2x+3\right).\left(bx+c\right)\)
\(\Leftrightarrow x^3+ax^2+5x+3=bx^3+\left(c+2b\right)x^2+\left(2c+3b\right)x+3c\)
\(\Rightarrow\left\{{}\begin{matrix}b=1\\c=1\end{matrix}\right.\). Đồng nhất hệ số, ta có: \(a=c+2b=1+2.1=3\)
Vậy \(a=3\)
Tìm a,b sao cho:
a,Đa thức x^4-x^3+6x^2-x+a chia hết cho x^2-x+5
b,Đa thức 2x^3-3x^2+x+a chia hết cho x+2
c,Đa thức 3x^3+ax^2+bx+9 chia hết cho x+3 và x-3
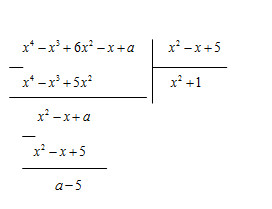
Vậy a = 5 thì đa thức x^4 - x^3 + 6x^2 - x +a chia hết cho đa thức x^2 - x + 5
Đúng 0
Bình luận (0)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)


 Chào bạn!
Chào bạn!
