cho x+y=1 tìm gtnn của M=x4+y4
TP
Những câu hỏi liên quan
Cho x,y la cac so duong thoa man : x+y≤1. Tim GTNN cua:
P=(x4+y4+1)(1/x4+1/y4+1)
Cho x,y la cac so duong thoa man : x+y≤1. Tim GTNN cua:
P=(x4+y4+1)(1/x4+1/y4+1)
Can gap mn oi!!!
\(P=\left(x^4+y^4+\dfrac{1}{256}+\dfrac{255}{256}\right)\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)\)
\(P=\left(x^4+y^4+\dfrac{1}{256}\right)\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)+\dfrac{255}{256}\left(\dfrac{1}{x^4}+\dfrac{1}{y^4}+1\right)\)
\(P\ge\left(\dfrac{x^2}{x^2}+\dfrac{y^2}{y^2}+\dfrac{1}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{2}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)^2+1\right)\)
\(P\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{2}\left(\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\right)^2+1\right)\)
\(P\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{1}{8}\left(\dfrac{4}{x+y}\right)^4+1\right)\ge\left(\dfrac{33}{16}\right)^2+\dfrac{255}{256}\left(\dfrac{4^4}{8}+1\right)=\dfrac{297}{8}\)
\(P_{min}=\dfrac{297}{8}\) khi \(x=y=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
cho x+y+z=3.Tính GTNN của P=x4+y4+z4+12(1-x)(1-y)(1-z)
Ta co:\(x^2+y^2+z^2\ge\frac{\left(x+y+z\right)^2}{3}=\frac{9}{3}=3\) ; \(xyz\le\frac{\left(x+y+z\right)^3}{27}=\frac{27}{27}=1\)
\(P=x^4+y^4+z^4+12\left(1-z-y+yz-x+xz+xy-xyz\right)\)
\(=x^4+y^4+z^4+12-12xyz-12\left(x+y+z\right)+12\left(xy+yz+zx\right)\)
\(\ge\frac{\left(x^2+y^2+z^2\right)^2}{3}+12-12.\frac{\left(x+y+z\right)^3}{27}-12.3+12\left(xy+yz+zx\right)\)
\(\ge3+12-12.1-36+4.\left(xy+yz+zx\right)\left(x+y+z\right)\)
\(\ge-33+4.\left(xy+yz+zx\right)\left(\frac{x+y+z}{xyz}\right)\)
\(=-33+4.\left(xy+yz+zx\right)\left(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}\right)\ge-33+4\left(xy.\frac{1}{xy}+yz.\frac{1}{yz}+zx.\frac{1}{zx}\right)^2\)
\(=-33+4\left(1+1+1\right)^2=-33+36=3\)
Dau '=' xay ra khi \(x=y=z=1\)
Vay \(P_{min}=3\)khi \(x=y=z=1\)
Đúng 1
Bình luận (0)
Tìm x, y biết
x
2
+
y
2
10
x
2
-
2
y
2
7
và x4.y4 81.
Đọc tiếp
Tìm x, y biết x 2 + y 2 10 = x 2 - 2 y 2 7 và x4.y4 = 81.
Đặt x2 = a (a ≥ 0), y2 = b (b ≥ 0)
Ta có: 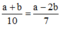 và a2b2 = 81.
và a2b2 = 81.
Theo tính chất của dãy tỉ số bằng nhau ta có:
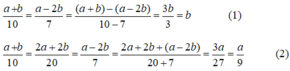
Từ (1) và (2) suy ra a/9 = b ⇒ a = 9b
Do a2b2 = 81 nên (9b)2.b2 = 81 ⇒ 81b4 = 81 ⇒ b4 = 1 ⇒ b = 1 (vì b ≥ 0)
Suy ra a = 9. 1 = 9
Ta có x2 = 9 và y2 = 1. Suy ra x = 3 hoặc x = -3, y = 1 hoặc y = -1.
Đúng 0
Bình luận (0)
với x1,x2,x3,x4,x5 thuộc R ,tổng là 300,gọi M là số lớn nhất trong các số x1+x2,x2+x3,x3+x4,x4+x5.tìm GTNN của M.
Giúp mình nha!
M là số lớn nhất trong các số x1+x2x2+x3,x3+x4,x4+x5,
suy ra;3M >=(x1+x2)+(x2+x3)+(x4+x5)
suy ra 3M >=300+X2
suy ra M>=100+X2/3>=100
Với x2=x4=0,x1=x3=x5=100 thì M =100
Vậy GTNN của M =100
Đúng 0
Bình luận (0)
cho x+y=1 tìm gtnn của M=x4+y4
giúp với mai mình thi ròi
\(M=\left(x^2+y^2\right)^2-2x^2y^2\)
\(M=\left[\left(x+y\right)^2-2xy\right]^2-2x^2y^2\)
Áp dụng BĐT Cauchy:
\(x+y\ge2\sqrt{xy}\)\(\Rightarrow xy\le\frac{1}{4}\)
\(\Rightarrow M\ge\left[1-\frac{1}{2}\right]^2-2.\frac{1}{16}\)\(=\frac{1}{8}\)
\(M_{min}=\frac{1}{8}\Leftrightarrow x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
dễ Cm được x² +y² ≥ (x+y)²/2
<=> x² +y² ≥ 1/2(x² +y²) + xy
<=> 1/2(x² +y²) -xy ≥ 0
<=> 1/2(x-y)² ≥ 0 ( luôn đúng )
vậy x² + y² ≥ (x+y)²/2 = 1/2
tương tự thì
x^4 + y^4 ≥ (x² +y²)²/2 ≥ (1/2)²/2 = 1/8
vậy x^4 + y^4 ≥ 1/8
dấu = xảy ra <=> x=y=1/2
Đúng 0
Bình luận (0)
c3: cho x+y=15, tìm giá tị nhỏ nhất , lớn nhất của biểu thức:
B=căn (x-4) + căn (y-3)
c4: tìm GTNN của biểu thức A= (2x^2 - 6x + 5) / 2x
c5: cho a, b, x là những số dương. tìm GTNN của :
P= [(x+a)(x+b)]/x
C3 : Ta có ; \(B=\sqrt{x-4}+\sqrt{y-3}\) . Nhận xét : \(B\ge0\)
Áp dụng bất đẳng thức Bunhiacopxki : \(B^2=\left(1.\sqrt{x-4}+1.\sqrt{y-3}\right)^2\le\left(1^2+1^2\right)\left(x-4+y-3\right)\)\(\Rightarrow B^2\le16\Rightarrow B\le4\). Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x\ge4,y\ge3\\\sqrt{x-4}=\sqrt{y-3}\\x+y=15\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=8\\y=7\end{cases}}\)
Vậy B đạt giá trị lớn nhất bằng 4 tại (x;y) = (8;7)
Tìm GTNN và mấy bài tới để từ từ mình làm cho nhé , tại mạng đang chậm...
Đúng 0
Bình luận (0)
C4 : Bạn cần thêm điều kiện x là số dương nhé : )
Ta có ; \(A=\frac{2x^2-6x+5}{2x}=x+\frac{5}{2x}-3\). Áp dụng bất đẳng thức Cauchy :
\(x+\frac{5}{2x}\ge2\sqrt{x.\frac{5}{2x}}=\sqrt{10}\). Dấu "=" xảy ra \(\Leftrightarrow x=\frac{5}{2x}\Leftrightarrow\sqrt{\frac{5}{2}}\)
Vậy Min A = \(\sqrt{10}-3\Leftrightarrow x=\sqrt{\frac{5}{2}}\)
C5 : Bạn cần thêm điều kiện a,b là hằng số nhé :)
\(P=\frac{\left(x+a\right)\left(x+b\right)}{x}=\frac{x^2+ax+bx+ab}{x}=x+\frac{ab}{x}+a+b\)
Áp dụng bất đẳng thức Cauchy : \(x+\frac{ab}{x}\ge2\sqrt{x.\frac{ab}{x}}=2\sqrt{ab}\Rightarrow P\ge a+2\sqrt{ab}+b=\left(\sqrt{a}+\sqrt{b}\right)^2\)
Dấu "=" xảy ra khi và chỉ khi \(x^2=ab\Leftrightarrow x=ab\) (vì a,b,x > 0)
Vậy .......
Đúng 0
Bình luận (0)
cho x>0,y>0 và x+y=2a
tìm GTNN của A = 1/x+1/y
Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)ta có \(A=\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}=\frac{4}{2a}=\frac{2}{a}\)
Min A = 2/a tại x = y = a
Đúng 0
Bình luận (0)


