cho hàm số y = f(x) = 1,4 - x
a/ tìm x, biết giá trị tuyệt đối của f(x) = 0
Cho hàm số y = f(x) = 1,4-x
tìm x biết giá trị tuyệt đối của f(x) = 0
Cho hàm số giá trị tuyệt đối: y=f(x)=|3x-1|
a/Tính f(-2) ; f(2) ; f(-1/4) ; f(1/4)
b/Tìm x,biết f(x)=10 ; f(x)= -3
a) Thay x=-2 vào hàm số f(x)=|3x-1|, ta được:
\(f\left(-2\right)=\left|3\cdot\left(-2\right)-1\right|=\left|-6-1\right|=7\)
Thay x=2 vào hàm số \(f\left(x\right)=\left|3x-1\right|\), ta được:
\(f\left(2\right)=\left|3\cdot2-1\right|=\left|6-1\right|=5\)
Thay \(x=-\dfrac{1}{4}\) vào hàm số \(f\left(x\right)=\left|3x-1\right|\), ta được:
\(f\left(-\dfrac{1}{4}\right)=\left|3\cdot\dfrac{-1}{4}-1\right|=\left|-\dfrac{3}{4}-\dfrac{4}{4}\right|=\dfrac{7}{4}\)
Thay \(x=\dfrac{1}{4}\) vào hàm số \(f\left(x\right)=\left|3x-1\right|\), ta được:
\(f\left(\dfrac{1}{4}\right)=\left|3\cdot\dfrac{1}{4}-1\right|=\left|\dfrac{3}{4}-1\right|=\dfrac{1}{4}\)
Vậy: f(-2)=7; f(2)=5; \(f\cdot\left(-\dfrac{1}{4}\right)=\dfrac{7}{4}\); \(f\left(\dfrac{1}{4}\right)=\dfrac{1}{4}\)
b) Để f(x)=10 thì \(\left|3x-1\right|=10\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=10\\3x-1=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=11\\3x=-9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{3}\\x=-3\end{matrix}\right.\)
Để f(x)=-3 thì \(\left|3x-1\right|=-3\)
mà \(\left|3x-1\right|\ge0\forall x\)
nên \(x\in\varnothing\)
Cho hàm số y = f(x) = \(\frac{1}{3}\)x
a, Tìm điều kiện để A thuộc đồ thị hàm số sao cho Ya + 2/Xa/ = 5
b, Tìm m để f(m) - 1 = 5
/ / là giá trị tuyệt đối
Cho hàm số y = f(x) = \(\frac{1}{3}\)x
a, Tìm điều kiện A thuộc đồ thị hàm số sao cho Ya + 2/Xa/ = 5
b, Tìm m để f(m)-1=5
/ / là giá trị tuyệt đối
Cho hàm số y = f(x) = \(\frac{1}{3}\)x
a,Tìm điều kiện A thuộc đồ thị hàm số sao cho Ya + 2/Xa/ = 5
b, Tìm m để f(m) - 1 = 5
/ / là giá trị tuyệt đối
Bài 2 : Cho hàm số f(x) xác định bởi công thức : y= f(x) = |x-1| - 2
Hãy viết hàm số về dạng không còn dấu giá trị tuyệt đối
Bài 3 : Cho hàm số : y = f(x) = | x+ 1 | + | x+ 5 | -6
Hãy viết công thức đã cho về dạng không còn dấu giá trị tuyệt đối . Từ đó tìm giá trị nhỏ nhất của hàm số
Câu 1: Cho hàm số y = 2x\(^2\)
a) Hãy lập bảng tính các giá trị f(-5), f(-3), f(0), f(3), f(5)
b) Tìm x biết f(x) = 8, f(x) = 6 - 4\(\sqrt{2}\)
Câu 2: Cho hàm số y = f(x) = \(\dfrac{1}{3}x^2\)
Tìm các giá trị của x, biết rằng \(y=\dfrac{1}{27}\). Cũng câu hỏi tương tự với y = 5
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
cho hàm số y=f(x) biết (x+10)*f(x+5)=f(x-4). Tìm 2 giá trị của x để f(x)=0
Cho hàm số y = f x có đồ thị như hình vẽ . Tìm tất cả các giá trị thực của tham số m để phương trình f x − m = 0 có đúng 2 nghiệm và giá trị tuyệt đối của 2 nghiệm này đều lớn hơn 1
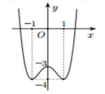
A. m > − 4
B. − 4 < m < − 3
C. m > − 3
D. − 4 < m ≤ − 3
Đáp án C
Khi m > -3 thì phương trình f(x) = m có hai nghiệm lớn hơn 1. Do đó chọn phương án C.