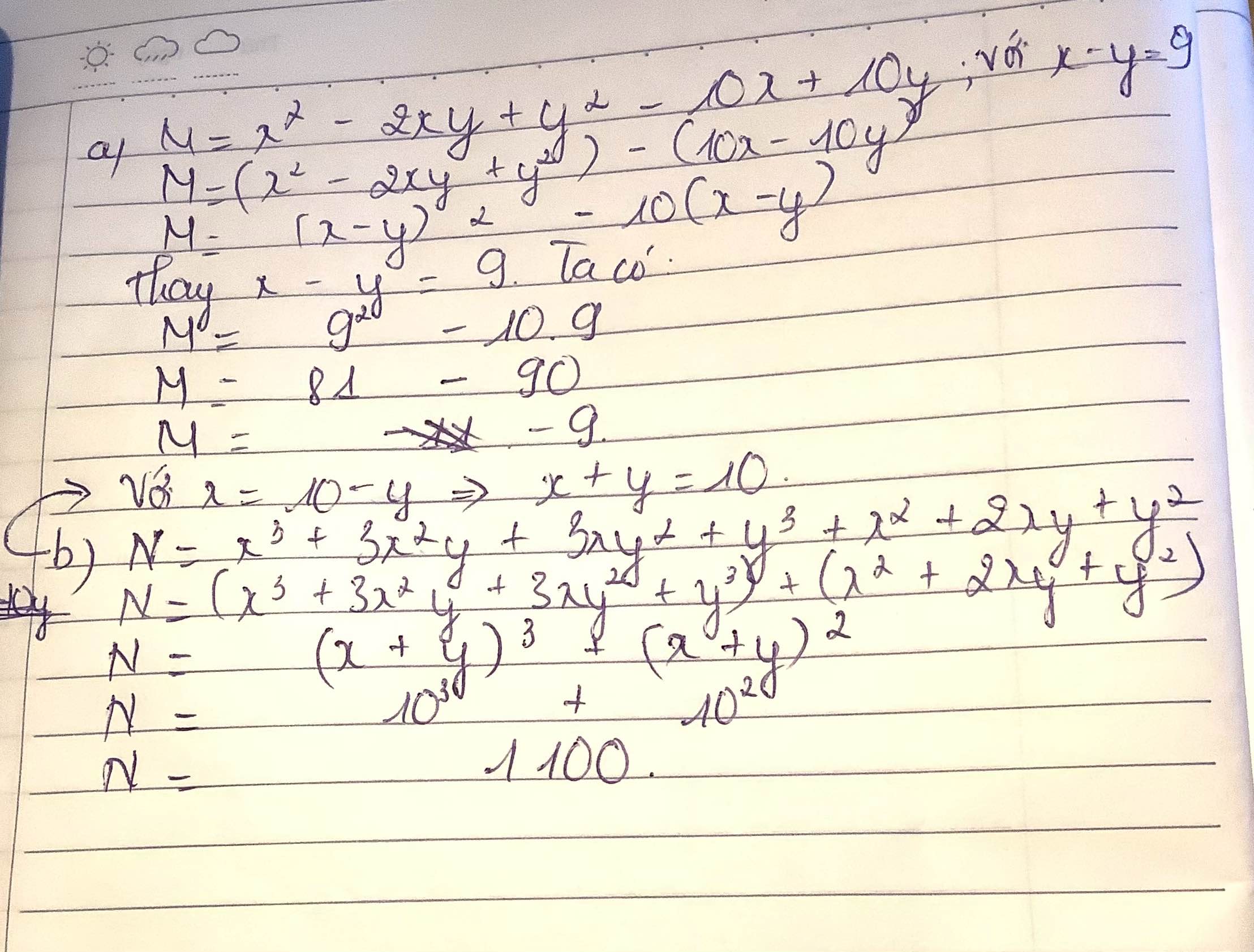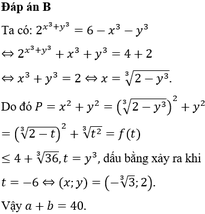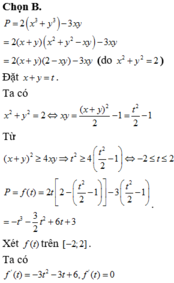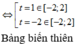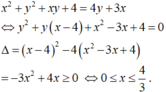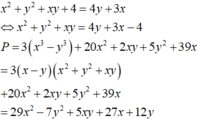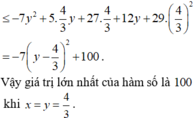cho hai số thực x,y thỏa mãn x3-3xy2=10 và y3-3x2y=30 . Tính giá trị biểu thức P=x2+y2
LH
Những câu hỏi liên quan
Tính giá trị biểu thức:
a) M=x2-2xy+y2-10x+10y với x-y=9
b) N=x3+3x2y+3xy2+y3+x2+2xy+y2 với x=10-y
a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)
Đúng 1
Bình luận (0)
Cho x 10 – y. Khi đó khẳng định nào sau đây là đúng khi nói về giá trị của biểu thức
N
x
3
+
3
x
2
y
+
3
x
y
2
+
y
3
+
x
2
+...
Đọc tiếp
Cho x = 10 – y. Khi đó khẳng định nào sau đây là đúng khi nói về giá trị của biểu thức N = x 3 + 3 x 2 y + 3 x y 2 + y 3 + x 2 + 2 x y + y 2
A. N > 1200
B. N < 1000
C. N < 0
D. N > 1000
Ta có
N = x 3 + 3 x 2 y + 3 x y 2 + y 3 + x 2 + 2 x y + y 2 = ( x 3 + 3 x 2 y + 3 x y 2 + y 3 ) + ( x 2 + 2 x y + y 2 ) = ( x + y ) 3 + ( x + y ) 2 = ( x + y ) 2 ( x + y + 1 )
Từ đề bài x = 10 – y ó x + y = 10. Thay x + y = 10 vào N = ( x + y ) 2 (x + y + 1) ta được
N = 10 2 (10 + 1) = 1100
Suy ra N > 1000 khi x = 10 – y
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho x,y là số dương thỏa mãn x+y<1. Tìm giá trị nhỏ nhất của biểu thức: A= 1/x3+3xy2 + 1/y3+3x2y
Cho hai số thực
x
,
y
∈
[
-
3
;
2
]
thỏa mãn
2
x
3
+
y
3
6
-
x
3
-
y
3
. Giá trị lớn nhất của biểu thức
P
x...
Đọc tiếp
Cho hai số thực x , y ∈ [ - 3 ; 2 ] thỏa mãn 2 x 3 + y 3 = 6 - x 3 - y 3 . Giá trị lớn nhất của biểu thức P = x 2 + y 2 có dạng a + b 3 ( a , b ∈ N ) . Hỏi a + b bằng bao nhiêu?
A. 30
B. 40
C. 36
D. 45
Cho hai số thực x, y thay đổi thỏa mãn điều kiện
x
2
+
y
2
2
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P
2
(
x
3
+
y
3
)
...
Đọc tiếp
Cho hai số thực x, y thay đổi thỏa mãn điều kiện x 2 + y 2 = 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 2 ( x 3 + y 3 ) - 3 x y . Giá trị của của M + m bằng
A. -4
B. - 1 2
C. -6
D. 1 - 4 2
Chọn B.
P =
2
(
x
3
+
y
3
)
-
3
x
y
(do
x
2
+
y
2
=
2
)
Đặt x + y = t. Ta có
x
2
+
y
2
=
2
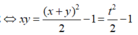
Từ 
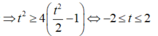
P = f(t)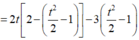 
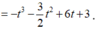
Xét f(t) trên [-2;2].
Ta có 
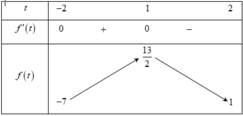
Bảng biến thiên
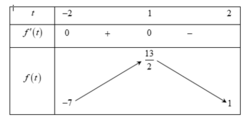
Từ bảng biến thiên ta có max P = max f(t) = 13 2 ; min P = min f(t) = -7
Lời bình: Có thể thay bbt thay bằng
Ta có 
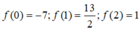
Suy ra kết luận.
Đúng 0
Bình luận (0)
Cho hai số thực x, y thay đổi thỏa mãn điều kiện
x
2
+
y
2
2
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P
2
(
x
3
+
y
3
)
-
3
x
y
. Giá trị của của M + m bằng A. -4 B. -...
Đọc tiếp
Cho hai số thực x, y thay đổi thỏa mãn điều kiện x 2 + y 2 = 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 2 ( x 3 + y 3 ) - 3 x y . Giá trị của của M + m bằng
A. -4
B. -1/2
C. -6
D. 1
Cho x,y là hai số thực thỏa mãn điều kiện
x
2
+
y
2
+
x
y
+
4
4
y
+
3
x
. Tìm giá trị lớn nhất của biểu thức
P
3
(
x...
Đọc tiếp
Cho x,y là hai số thực thỏa mãn điều kiện x 2 + y 2 + x y + 4 = 4 y + 3 x . Tìm giá trị lớn nhất của biểu thức P = 3 ( x 3 - y 3 ) + 20 x 2 + 2 x y + 5 y 2 + 39 x .
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy (1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P1√1+x2 +1√1+y2 +4xy−x2−y2
Đọc tiếp
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy =(1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P=1√1+x2 +1√1+y2 +4xy−x2−y2
Không nhìn thấy bất cứ chữ nào của đề bài cả
Đúng 1
Bình luận (0)
H24
SGK Kết nối tri thức và cuộc sống
21 tháng 7 2023 lúc 15:38
Phân tích các đa thức sau thành nhân tử:
a) x3+y3+x+y
b) x3−y3+x−y
c) (x−y)3+(x+y)3
d) x3−3x2y+3xy2−y3+y2−x2
`a, x^3 + y^3 + x + y`
`= (x+y)(x^2-xy+y^2)+x+y`
`= (x+y)(x^2-xy+y^2+1)`
`b, x^3 - y^3 + x -y`
`= (x-y)(x^2+xy+y^2)+x-y`
`= (x-y)(x^2+xy+y^2+1)`
`c, (x-y)^3 + (x+y)^3`
`= (x-y+x+y)(x^2-2xy+y^2 - x^2 + y^2 + x^2 + 2xy + y^2)`
`= (2x)(x^2 + 3y^2)`
`d, x^3 - 3x^2y + 3xy^2 - y^3 + y^2 - x^2`
`= (x-y)^3 + (y-x)(x+y)`
`=(x-y)(x^2+2xy+y^2-x-y)`
Đúng 1
Bình luận (0)
a: =(x+y)(x^2-xy+y^2)+(x+y)
=(x+y)(x^2-xy+y^2+1)
b: =(x-y)(x^2+xy+y^2)+(x-y)
=(x-y)(x^2+xy+y^2+1)
c: =x^3-3x^2y+3xy^2-y^3+x^3+3x^2y+3xy^2-y^3
=2x^3+6xy^2
d: =(x-y)^3+(y-x)(y+x)
=(x-y)[(x-y)^2-(x+y)]
Đúng 0
Bình luận (0)
Cho hai số x,y \(\ge\)0 thay đổi và thỏa mãn x+y=2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P= x(x3 + x2 + x + 1004y) + y(y3 + y2 + y +1004x) + 1