BT: Cho ΔABC vuông ở A có trung tuyến AM. C/m: AM = 1/2.BC
XL
Những câu hỏi liên quan
Cho ΔABC vuông tại A, trung tuyến AM. Từ B kẻ BH vuông góc AM (H thuộc AM) và cắt AC tại D
a) CM: ΔBAD \(\sim\) ΔBHA. Từ đó suy ra AB2 = BH.BD
b) CM: AD.AC = BH.BD
c) Từ D kẻ DE // BC (E thuộc AB) cắt AM ở I. CM : I là trung điểm của DE
a) Xét ΔBAD vuông tại A và ΔBHA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔBAD\(\sim\)ΔBHA(g-g)
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BD}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BH\cdot BD\)(đpcm)
Đúng 0
Bình luận (0)
cho ΔABC có AB=AC. Gọi M là trung điểm của BC. Chứng minh rằng:
a) ΔAMB=ΔAMC
b) AM là tia phân giác của góc BAC
c) AM vuông góc BC
d) Vẽ At là tia phân gác của góc ngoài ở đỉnh A của ΔABC. Chứng minh: At//BC
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Đúng 0
Bình luận (0)
Cho ΔABC có AB=5cm, AC=12cm, BC=13cm. Gọi AM là đường trung tuyến của ΔABC
a) Chứng minh: ΔABC vuông. từ đó tính Am?
b) Kẻ MD⊥AB, ME⊥AC. Chứng minh AM=DE
c) Chứng minh DE là đường trung bình của ΔABC. Từ đó suy ra tứ giác BDEC là hình gì?
a: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
AM=BC/2=6,5cm
b: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADMElà hình chữ nhật
=>AM=DE
c: Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của BA
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do do: E là trung điểm của AC
Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
nên DE là đường trung bình
=>DE//BC
=>BDEC là hình thang
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A có M là trung điểm của BC. Chứng minh AM=\(\frac{1}{2}BC\).
trong tg vuông dg trung tuyen thuoc canh huyen = 1/2 canh huyen
( sach gk có cm)
Đúng 0
Bình luận (0)
tam giác ABC vuông tại A.trung tuyến AM, M là trung điểm BC thì ta có AM = 1/2 BC. tam giác ABC bất kí mà trung tuyến AM = 1/2 BC thì có suy ra được tam giác ABC vuông tại A hay không ?
Cho ΔABC vuông tại A, kẻtrung tuyến AM( Mthuộc BC). KẻMI //AB, MK //AC.
a) Tứgiác AIMKlà hình gì. Vì sao?
b) Gọi O là trung điểm AM. Chứng minh I,O,K thẳng hàng.
c) Tìm điều kiện của ΔABC đểtứgiác AIMKlà hình vuông
cho ΔABC vuông tại A . có đường trung tuyến AM . Đường trung tuyến của cạnh BC cắt AC tại D . Trên tia đối của tia AC lấy E sao cho AE=AD. gọi N là giao điểm của BE và AM. so sánh BN và AC
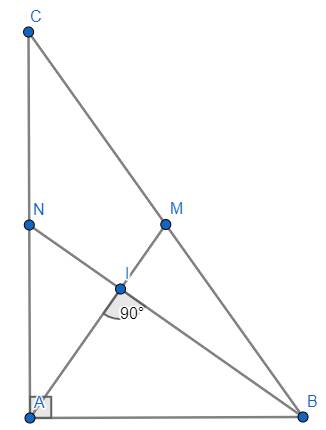
Cho ΔABC vuông tại A, AB = a. Các đường trung tuyến AM và BN vuông góc với nhau. Tính AB và BC theo a.
Gọi \(I\) là giao điểm của \(AM\) và \(BN\Rightarrow IB=\dfrac{2}{3}BN;IN=\dfrac{1}{3}BN;AI=\dfrac{2}{3}AM;IM=\dfrac{1}{3}AM\)
\(\Delta ANB\) vuông tại \(A:AI^2=IB.IN\) \(\Rightarrow AI^2=\dfrac{2}{3}BN\cdot\dfrac{1}{3}BN=\dfrac{2}{9}BN^2\)
Ta cũng có trong \(\Delta ANB:AB^2=IB.BN\)
\(\Leftrightarrow a^2=\dfrac{2}{3}BN\cdot BN=\dfrac{2}{3}BN^2\Leftrightarrow BN^2=\dfrac{3}{2}a^2\)
Suy ra : \(AI^2=\dfrac{2}{9}BN^2=\dfrac{2}{9}\cdot\dfrac{3}{2}a^2=\dfrac{1}{3}a^2\).
Lại có : \(AI=\dfrac{2}{3}AM\Rightarrow AM^2=\dfrac{9}{4}AI^2=\dfrac{9}{4}\cdot\dfrac{1}{3}a^2=\dfrac{3}{4}a^2\)
\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) của \(\Delta ABC\) vuông tại \(A\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC^2=4AM^2=4\cdot\dfrac{3}{4}a^2=3a^2\)
\(\Rightarrow BC=\sqrt{3a^2}=a\sqrt{3}\)
\(\Delta ABC\) vuông tại \(A\) có : \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{3a^2-a^2}=a\sqrt{2}\)
Vậy : \(AC=a\sqrt{2};BC=a\sqrt{3}\)
Đúng 1
Bình luận (0)
* Cho ΔABC vuông tại A có B= \(30^0\), AB=6cm
a. Giải ΔABC
b. Vẽ đường cao AH và trung tuyến AM của ΔABC. Tính diện tích ΔAHM
* Cho ΔABC vuông tại A có AB=3 cm, BC=5cm, đường cao AH
a. Tính số đo góc B, C
b. Gọi AE là phân giác của góc A (E ∈ BC). Tính AE
Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)