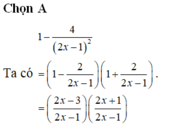Biết rằng f(1/2)=a ;f(√3/2)=b và x + xf'(x)=2f(x) -4 .tính tích phân cận từ (π/6 đến π/3) của biểu thức[ (sinx^2*cosx + 2sin2x)]/[f(sinx)]^2 theo a và b
H24
Những câu hỏi liên quan
a,Cho đa thức f(x)=ax+b (a khác 0). Biết f(0)=0, chứng minh rằng F(x)=-f(-x)với mọi x
b,Đa thức f(x)=ax^2=bx+c (a khác 0).Biết F(1)=F(-1), chứng minh rằng f(x) với mọi x
a)Cho hàm số f(x)=ax^2+bx+c là các số hữu thỉ .Chứng tỏ rằng f(-2),f(3)lớn hơn hoặc bằng 0 biết rằng 13a+b+2c=0
b)Cho hàm số f(x) xác định với mọi x thuộc R .Biết rằng với mọi x ta đều có f(x)+3*f(1/x)=x^2
T Nc cđ :
Bài 2: Cho đa thức f(x) thỏa mãn điều kiện: x.f(x + 1) = (x + 2).f(x). Chứng minh rằng đa thức f(x) có ít nhất hai nghiệm.
Bài 3: Cho hàm số f(x) = ax^2 + bx + c (a, b, c ∈ Z}). Biết f(-1) ⋮ 3; f(0) ⋮ 3; f(1) ⋮ 3. Chứng minh rằng a, b, c đều chia hết cho 3.
Bài 4: Cho đa thức f(x) = ax^3 + bx^2 + cx + d với a là số nguyên dương và f(5) - f(4) = 2019. Chứng minh f(7) - f(2) là hợp số.
Bài 4:
\(f\left(5\right)-f\left(4\right)=2019\)
=>\(125a+25b+25c+d-64a-16b-4c-d=2019\)
=>\(61a+9b+21c=2019\)
\(f\left(7\right)-f\left(2\right)\)
\(=343a+49b+7c+d-8a-4b-2c-d\)
\(=335a+45b+5c\)
\(=5\left(61a+9b+21c\right)=5\cdot2019\) là hợp số
Đúng 0
Bình luận (0)
Tìm hệ số a và b của đa thức f(x)= ax+b biết rằng f(1)=1,f(2)=4
ta có: f(1)=a.1+b=a+b
do f(1)=1 nên a+b=1 (1)
lại có: f(2)=a.2+b=2a+b
do f(2)=4 nên 2a+b=4 (2)
từ (1) (2) => a=3; b=-2
Tính các hệ số a và b của đa thức f(x) =ax + b biết rằng f(1) = 1 , f(2) = 4.
Giải
Vì f(1) = 1 nên ta có a*1 +b =1 <=> a+b =1 (1)
Tương tự ta có f(2)=4 <=> 2a+ b = 4 (2)
Từ (1) và (2) ta giải được a = 3, b= -2
Đúng 0
Bình luận (0)
Cho f(x) = ax^1 + bx + c với a,b,c là các số hữu tỉ . Chứng tỏ rằng f(-2) . f(3) < hoặc = 0 . Biết rằng 13a + b + 2c = 0
Ta có:
f(−2)+f(3)=((−2)2a−2b+c)+(32a+3b+c)=(4a−2b+c)+(9a+3b+c)=13a+b+2c=0f(−2)+f(3)=((−2)2a−2b+c)+(32a+3b+c)=(4a−2b+c)+(9a+3b+c)=13a+b+2c=0
Suy ra⎡⎢ ⎢ ⎢ ⎢⎣{f(−2)>0f(3)<0{f(−2)<0f(3)>0⇒f(−2).f(3)<0
vậy......
Đúng 0
Bình luận (0)
\(13a+b+2c=0\Rightarrow b=-13a-2c\)
\(f\left(x\right)=ax^2+bx+c\)
\(f\left(-2\right).f\left(3\right)=\left(4a-2b+c\right)\left(9a+3b+c\right)\)
\(=\left(4a-2\left(-13a-2c\right)+c\right)\left(9a+3\left(-13a-2c\right)+c\right)\)
\(=\left(4a+26a+4c+c\right)\left(9a-39a-6c+c\right)\)
\(=\left(30a+5c\right)\left(-30a-5c\right)\)
\(=-\left(30a+5c\right)^2\le0\)
-Dấu "=" xảy ra khi \(a=-b=-\dfrac{1}{6}c\)
Đúng 1
Bình luận (0)
dấu bằng xảy ra khi a = -b = -1/6c
Đúng 0
Bình luận (0)
cho đa thức f(x)=a4x4+a3x3+a2x2+a1x+a0
biết rằng f(1)=f(-1);f(2)=f(-2)
chứng minh f(x)=f(-x) với mọi x
Cho hàm số
f
(
x
)
ln
(
1
-
4
(
2
x
-
1
)
2
)
. Biết rằng
f
(
2
)
+
f
(
3
)
+
.
.
.
+
f
(...
Đọc tiếp
Cho hàm số f ( x ) = ln ( 1 - 4 ( 2 x - 1 ) 2 ) . Biết rằng f ( 2 ) + f ( 3 ) + . . . + f ( 2020 ) = ln a b , trong đó a b là phân số tối giản, a , b ∈ N * . Tính b -3a
A. -2
B. 3
C. -1
D. 1
cho đa thức f(x) = ax2 + bx +c với a,b,c là các số thực .Biết rằng f(0) ; f(1) ; f(2) có giá trị nguyên . Chứng minh rằng 2a, 2b có giá trị nguyên
\(f\left(0\right)=a.0^2+b.0+c=c\) có giá trị nguyên
\(f\left(1\right)=a+b+c\) có giá trị nguyên => a + b có giá trị nguyên
\(f\left(2\right)=4a+2b+c=2a+2\left(a+b\right)+c\)=> 2a có giá trị nguyên
=> 4a có giá trị nguyên
=> 2b có giá trị nguyên.
a
cho f(x) = \(ax^2+bx+c\) ( a ; b ; c ∈Q )
Biết f(0) ; f(1) ; f(2) có giá trị nguyên.
chứng minh rằng 2a , 2b có giá trị nguyên
Lời giải:
$f(0)=a.0^2+b.0+c=c$ nguyên
$f(1)=a+b+c$ nguyên, mà $c$ nguyên nên $a+b+c-c=a+b$ nguyên
$f(2)=4a+2b+c=2a+2(a+b)+c$ nguyên mà $a+b, c$ nguyên nên $2a$ nguyên
$2a$ nguyên, $2(a+b)$ nguyên nên $2b$ nguyên.
Ta có đpcm.
Đúng 2
Bình luận (0)