Cho tam giác DEF vuông tại D viết tỉ lượng giác của góc E. Từ đó suy ra cách tính DE,DF,EF
TB
Những câu hỏi liên quan
Cho tam giác DEF vuông tại D có DE =5cm, DF =12cm. Tính các tỉ số lượng giác của góc E từ đó suy ra các tỉ số lượng giác của góc F
Lời giải:
$EF=\sqrt{ED^2+DF^2}=\sqrt{5^2+12^2}=13$ (cm) theo định lý Pitago
$\sin E=\frac{DF}{EF}=\frac{12}{13}$
$\cos E=\frac{ED}{EF}=\frac{5}{13}$
$\tan E=\frac{DF}{ED}=\frac{12}{5}$
$\cot E=\frac{1}{\tan E}=\frac{5}{12}$
Vì $\widehat{E}, \widehat{F}$ là 2 góc phụ nhau nên:
$\sin F=\cos E=\frac{5}{13}$
$\cos F=\sin E=\frac{12}{13}$
$\tan F=\cot E=\frac{5}{12}$
$\cot F=\tan E=\frac{12}{5}$
Đúng 1
Bình luận (0)
Cho tam giác DEF vuông tại D có DE=0,9cm ; DF=12cm và DH vuông góc với EF a) Viết tỉ số lượng giác tan E b) tính các tỉ số lượng giác của góc F
a: ΔDEF vuông tại D
=>\(DE^2+DF^2=EF^2\)
=>\(EF^2=0,9^2+12^2=144,81\)
=>\(EF=\sqrt{144,81}\)(cm)
Xét ΔDEF vuông tại D có \(tanE=\dfrac{DF}{DE}\)
=>\(tanE=\dfrac{12}{0,9}=\dfrac{120}{9}=\dfrac{40}{3}\)
b: Xét ΔDEF vuông tại D có
\(sinF=\dfrac{DE}{EF}=\dfrac{0.9}{\sqrt{144,81}}\)
\(cosF=\dfrac{DF}{EF}=\dfrac{12}{\sqrt{144,81}}\)
\(tanF=\dfrac{0.9}{12}=\dfrac{9}{120}=\dfrac{3}{40}\)
\(cotF=\dfrac{12}{0.9}=\dfrac{40}{3}\)
Đúng 2
Bình luận (0)
Cho tam giác DEF cân tại D. Gọi M,N lần lượt là trung điểm của DF và DE. Kẻ DH vuông góc với EF (H thuộc EF)
a) C/m HE =HF
b) Cho DE=DF=5, EF=6. Tính DH
c) C/m tam giác DME = tam giác DNF. Từ đó suy ra góc DEM = góc DFN
a: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của FE
hay HF=HE
b: EF=6cm nên HF=3cm
=>DH=4cm
c: Xét ΔDME và ΔDNF có
DM=DN
\(\widehat{EMD}\) chung
DE=DF
Do đó: ΔDME=ΔDNF
Đúng 2
Bình luận (0)
cho tam giác DEF vuông tại D có DE = 12 cm EF = 20 cm Kẻ DH vuông góc EF (H thuộc EF.)
a, Tính DF
b, Chứng minh tam giác EDF đồng dạng với tam giác DHF. Từ đó suy ra DF^2=FH.EF
Theo định lí Pytago tam giác DEF vuông tại D
\(DF=\sqrt{EF^2-DE^2}=16cm\)
b, Xét tam giác EDF và tam giác DHF
^DFE _ chung
^EDF = ^DHF = 900
Vậy tam giác EDF ~ tam giác DHF (g.g)
\(\dfrac{EF}{DF}=\dfrac{DF}{HF}\Rightarrow DF^2=EF.HF\)
Đúng 1
Bình luận (0)
a: \(DF=\sqrt{20^2-12^2}=16\left(cm\right)\)
b: Xét ΔEDF vuông tại D và ΔDHF vuông tại H có
góc F chung
Do đó: ΔEDF\(\sim\)ΔDHF
Đúng 1
Bình luận (0)
2.
cho tam giác DEF vuông tại D có DE = 12 cm EF = 20 cm Kẻ DH vuông góc EF (H thuộc EF.)
a, Tính DF
b, Chứng minh tam giác EDF đồng dạng với tam giác DHF. Từ đó suy ra DF^2=FH.EF
Xem chi tiết
cho tam giác DEF vuông tại D có DE = 12 cm EF = 20 cm Kẻ DH vuông góc EF (H thuộc EF.)
a, Tính DF
b, Chứng minh tam giác EDF đồng dạng với tam giác DHF. Từ đó suy ra DF^2=FH.EF
TRẢ LỜI NHANH trong 10 PHÚT và Nhận thưởng
a, Theo định lí Pytago tam giác DEF vuông tại D
\(DF=\sqrt{EF^2-DE^2}=16cm\)
b, Xét tam giác EDF và tam giác DHF có
^EFD _ chung, ^EDF = ^DHF = 900
Vậy tam giác EDF ~ tam giác DHF (g.g)
\(\dfrac{EF}{DF}=\dfrac{DF}{HF}\Rightarrow DF^2=EF.HF\)
Đúng 0
Bình luận (0)
Cho tam giác DEF vuông tại D . Trên cạnh EF lấy điểm A sao cho ED = EA, từ A vẽ đường vuông góc với EF cắt cạnh DF tại B và Cắt cạnh DE kéo dài tại C
A) Tam giác ADE là tam giác gì? Vì sao?
B)Chứng minh: tam giác DEB = tam giác AEB , từ đó suy ra: DB = AB
C)Chứng minh: BF > BD
a: Xét ΔEDA có ED=EA
nên ΔEDA cân tại E
b: Xét ΔDEB vuông tại D và ΔAEB vuông tại A có
BE chung
ED=EA
DO đó: ΔDEB=ΔAEB
Suy ra: DB=AB
Đúng 0
Bình luận (0)
Tam giác DEF vuông tựi D, đường cao DK. Biết DE=15,DF=25 a) Tính DK, EF b) Tính tỉ số lượng giác của góc F C) Tính góc E, F
tam giác DEF cân tại D có DE=DF=5cm, EF=6cm. Tia phân giác của góc E cắt DF tại M, phân giác của góc F cắt DE tại N. Tính DM. Tính tỉ số diện tích của ∆DMN và ∆DEF
a) Xét ΔDEF có
EM là đường phân giác ứng với cạnh DF(gt)
nên \(\dfrac{DM}{DE}=\dfrac{MF}{EF}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{DM}{5}=\dfrac{MF}{6}\)
mà DM+MF=DF(M nằm giữa D và F)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DM}{5}=\dfrac{MF}{6}=\dfrac{DM+MF}{5+6}=\dfrac{DF}{11}=\dfrac{5}{11}\)
Do đó:
\(\dfrac{DM}{5}=\dfrac{5}{11}\)
hay \(DM=\dfrac{25}{11}cm\)
Vậy: \(DM=\dfrac{25}{11}cm\)
Đúng 0
Bình luận (0)
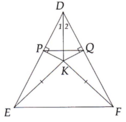
Cho tam giác DEF có DE = DF. Lấy điểm K nằm trong tam giác sao cho KE = KF. Kẻ KP vuông góc với DE (P thuộc DE), KQ vuông góc với DF (Q thuộc DF). Chứng minh:
a) K thuộc đường trung trực của EF và PQ;
b) DK là đường trung trực của EF và PQ. Từ đó suy ra PQ//EF.