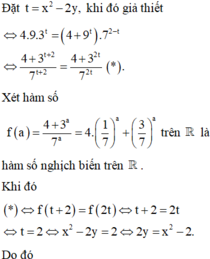cho x,y là hai số thực dương thỏa mãn đẳng thức x+y=2.Tìm GTLN của biểu thức M=x^2y^2(x^2+y^2)
TD
Những câu hỏi liên quan
cho x,y là hai số thực dương thỏa mãn x+y≤xy.Tìm giá trị lớn nhất của biểu thức M=\(\dfrac{1}{2x^2+3y^2}+\dfrac{1}{3x^2+2y^2}\)
\(x+y\le xy\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}\le1\)
\(M=\dfrac{1}{2\left(x^2+y^2\right)+y^2}+\dfrac{1}{2\left(x^2+y^2\right)+x^2}\le\dfrac{1}{4xy+y^2}+\dfrac{1}{4xy+x^2}\)
\(B\le\dfrac{1}{25}\left(\dfrac{4}{xy}+\dfrac{1}{y^2}\right)+\dfrac{1}{25}\left(\dfrac{4}{xy}+\dfrac{1}{x^2}\right)=\dfrac{1}{25}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{2}{xy}+\dfrac{6}{xy}\right)\)
\(M\le\dfrac{1}{25}\left[\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2+\dfrac{3}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\right]=\dfrac{1}{10}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le\dfrac{1}{10}\)
\(M_{max}=\dfrac{1}{10}\) khi \(x=y=2\)
Đúng 2
Bình luận (2)
Cho x, y, z là các số dương thỏa mãn: \(x^{2011}+y^{2011}+z^{2011}=3\). Tìm GTLN của biểu thức: \(M=x^2+y^2+z^2\)
Cho x, y, z là các số dương thỏa mãn: \(x^{2011}+y^{2011}+z^{2011}=3\). Tìm GTLN của biểu thức: \(M=x^2+y^2+z^2\)
\(x^{2011}+x^{2011}+1+...+1\) (2009 số 1) \(\ge2011\sqrt[2011]{x^{4022}}=2011x^2\)
Tương tự:
\(2y^{2011}+2009\ge2011y^2\); \(2z^{2011}+2009\ge2011z^2\)
Cộng vế:
\(2\left(x^{2011}+y^{2011}+z^{2011}\right)+6027\ge2011\left(x^2+y^2+z^2\right)\)
\(\Rightarrow2011\left(x^2+y^2+z^2\right)\le6033\)
\(\Rightarrow x^2+y^2+z^2\le3\)
Đúng 2
Bình luận (0)
Cho hai số thực dương x, y thỏa mãn \(2^x+2^y=4\). Tìm giá trị lớn nhất Pmax của biểu thức \(P=\left(2x^2+y\right)\left(2y^2+x\right)+9xy\)
\(4=2^x+2^y\ge2\sqrt{2^{x+y}}\Rightarrow2^{x+y}\le4\Rightarrow x+y\le2\)
\(\Rightarrow xy\le1\)
\(P=4x^2y^2+2x^3+2y^3+10xy\)
\(P=4x^2y^2+10xy+2\left(x+y\right)\left[\left(x+y\right)^2-3xy\right]\)
\(P\le4x^2y^2+10xy+4\left(4-3xy\right)=4x^2y^2-2xy+16\)
Đặt \(xy=t\Rightarrow0< t\le1\)
Xét hàm \(f\left(t\right)=4t^2-2t+16\) trên \((0;1]\)
\(\Rightarrow...\)
Đúng 2
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
5
x
+
2
y
+
3
3
x
y
+
x
+
1
5
x
y
5
+
3
−
x...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 − x − 2 y + x − 2 . Tìm giá trị nhỏ nhất của biểu thức T = x + y .
A. T min = 2 + 3 2 .
B. T min = 1 + 5 .
C. T min = 3 + 2 3 .
D. T min = 5 + 3 2 .
Đáp án C.
Ta có:
G T ⇔ 5 x + 2 y + x + 2 y − 3 − x − 2 y = 5 x y − 1 − 3 1 − x y + x y − 1.
Xét hàm số
f t = 5 t + t − 3 − t ⇒ f t = 5 t ln 5 + 1 + 3 − t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra f x + 2 y = f x y − 1 ⇔ x + 2 y = x y − 1
⇔ x = 2 y + 1 y − 1 ⇒ T = 2 y + 1 y − 1 + y . Do x > 0 ⇒ y > 1
Ta có: T = 2 + y + 3 y − 1 = 3 + y − 1 + 3 y − 1 ≥ 3 + 2 3 .
Đúng 0
Bình luận (0)
Cho x, y là các số thực dương thỏa mãn
5
x
+
2
y
+
3
3
x
y
+
x
+
1
5
x
y
5
+
3
-
x...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn 5 x + 2 y + 3 3 x y + x + 1 = 5 x y 5 + 3 - x - 2 y + x - 2 . Tìm giá trị nhỏ nhất của biểu thức T = x + y.
![]()
![]()
![]()
![]()
Đáp án C.
Ta có: GT
<=> 5x+2y + x + 2y – 3–x–2y = 5xy–1 – 31–xy + xy – 1.
X é t h à m s ố f t = 5 t + t - 3 - t
⇒ f t = 5 t ln 5 + 1 + 3 - t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra
f(x+2y) = f(xy – 1) <=> x+ 2y = xy – 1
⇔ x = 2 y + 1 y - 1 ⇒ T = 2 y + 1 y - 1 + y .
Do x > 0 => y > 1.
Ta có:
T = 2 + y + 3 y - 1 = 3 + y - 1 + 3 y - 1 ≥ 3 + 2 3 .
Đúng 0
Bình luận (0)
Cho ba số thực dương x, y, z thỏa mãn: \(x+2y+3z=2\). Tìm GTLN của biểu thức: \(S=\sqrt{\dfrac{xy}{xy+3z}+}\sqrt{\dfrac{3yz}{3yz+x}+}\sqrt{\dfrac{3xz}{3xz+4y}}\)
a) \(\left\{{}\begin{matrix}a=x\\b=2y\\c=3z\end{matrix}\right.\Rightarrow a+b+c=2;a,b,c>0\)
\(\Rightarrow S=\sqrt{\dfrac{\dfrac{ab}{2}}{\dfrac{ab}{2}+c}}+\sqrt{\dfrac{\dfrac{bc}{2}}{\dfrac{bc}{2}+a}}+\sqrt{\dfrac{ca}{ca+2b}}\)
\(=\sqrt{\dfrac{ab}{ab+2c}}+\sqrt{\dfrac{bc}{bc+2a}}+\sqrt{\dfrac{ca}{ca+2b}}\)
Vì a,b,c>0 nên áp dụng BĐT AM-GM, ta có:
\(\sqrt{\dfrac{ab}{ab+2c}}=\sqrt{\dfrac{ab}{ab+\left(a+b+c\right)c}}=\sqrt{\dfrac{ab}{c^2+bc+ca+ab}}=\sqrt{\dfrac{ab}{\left(a+c\right)\left(b+c\right)}}\)
\(=\sqrt{\dfrac{a}{a+c}}.\sqrt{\dfrac{b}{b+c}}\le\dfrac{1}{2}\left(\dfrac{a}{a+c}+\dfrac{b}{b+c}\right)\)
\(\sqrt{\dfrac{bc}{bc+2a}}=\sqrt{\dfrac{bc}{\left(b+a\right)\left(c+a\right)}}\le\dfrac{1}{2}\left(\dfrac{b}{a+b}+\dfrac{c}{a+c}\right)\)
\(\sqrt{\dfrac{ca}{ca+2b}}=\sqrt{\dfrac{ca}{\left(c+b\right)\left(a+b\right)}}\le\dfrac{1}{2}\left(\dfrac{c}{b+c}+\dfrac{a}{a+b}\right)\)
\(\Rightarrow S\le\dfrac{1}{2}\left(\dfrac{a}{a+b}+\dfrac{b}{a+b}\right)+\dfrac{1}{2}\left(\dfrac{b}{b+c}+\dfrac{c}{b+c}\right)+\dfrac{1}{2}\left(\dfrac{a}{a+c}+\dfrac{c}{a+c}\right)=\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi và chỉ khi: a=b=c=2/3=>\(\left(x,y,z\right)=\left\{\dfrac{2}{3};\dfrac{1}{3};\dfrac{2}{9}\right\}\)
Đúng 2
Bình luận (0)
Cho x,y là hai số dương thỏa mãn \(xy=1\). Tìm GTLN của biểu thức \(M=\frac{x}{x^4+y^2}+\frac{y}{x^2+y^4}\)
Cho \(xy=1\)và \(x,y>0\)
Tìm \(M_{max}=\frac{x}{x^4+y^2}+\frac{y}{x^2+y^4}\)
\(M=\frac{x}{x^4+\frac{1}{x^2}}+\frac{x}{y^2+\frac{1}{y^2}}\)
\(M=\frac{x^4}{x^6+1}+\frac{y^3}{y^6+1}\)
Áp dụng BĐT Cauchy
\(x^6+1\ge2x^3=>\frac{x^2}{x^6+1}\le\frac{1}{2}\)
Tương tự \(\frac{y^3}{y^6+1}\le\frac{1}{2}\)
\(=>M\le1\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}xy=1\\x=1\\y=1\end{cases}}\Leftrightarrow x=y=1\)
Vậy \(M_{max}=1\)khi \(x=y=1\)
Cho x, y là hai số thực dương thỏa mãn điều kiện
4
+
9.3
x
2
−
2
y
4
+
9
x
2
−
2
y...
Đọc tiếp
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9.3 x 2 − 2 y = 4 + 9 x 2 − 2 y .7 2 y − x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
A. P = 3 + 2 2
B. P = 1 + 9 2
C. P = 9
D. Không tồn tại