Cho tam giác ABC vuông tại A có AB=3cm, AC=4cm, Gọi P,Q lần lượt là trung điểm của AB,AC. Tính PQ
NT
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Gọi E,F lần lượt là trung điểm của AB,AC. Biết AB=3cm,A. C=4cm. Tính độ dài cạnh
Cho tam giác ABC vuông tại A có AB>AC và AH vuông góc với BC tại H. Gọi P, Q là hình chiếu vuông góc của H trên AB, AC.
a, Tứ giác APHQ là hình gì? Tại sao?
b, Chứng minh tam giác APQ đồng dạng với tam giác ACB.
c, Gọi I, K lần lượt là trung điểm của BH, CH. Chứng minh PI//QK.
d, Cho AB=4cm, AC=3cm. Tính diện tích tứ giác APHQ.
Cho tam giác ABC vuông tại A có AB = 3cm; BC = 5cm. Kẻ đường cao AH. Gọi P, Q lần lượt là hình chiếu của H trên AB và AC
b) Tính số đo góc B, góc C. Tính PQ
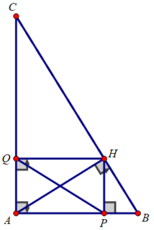
b)Xét tam giác ABC vuông tại A có:
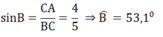
∠B + ∠C = 90 0 ⇒ ∠C = 90 0 - 53 , 1 0 = 36 , 9 0
Xét tứ giác APHQ có:
∠(PAQ) = ∠(AQH) = ∠(APH) = 90 0
⇒ Tứ giác APHQ là hình chữ nhật
⇒ PQ = AH = 12/5 (cm)
Đúng 0
Bình luận (0)
Bài 6. Cho tam giác ABC cân tại A có AB = AC = 6 cm, BC = 5 cm. Gọi D, E lần lượt là trung điểm của AB và AC. Gọi P, Q lần lượt là trung điểm của BD và CE. a) Chứng minh rằng: tứ giác BCED là hình thang cân. b) Tính độ dài đoạn thẳng PQ.
a: Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Do đó: DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BDEC là hình thang cân
Đúng 1
Bình luận (2)
Cho tam giác ABC vuông tại A có AB 3cm, AC 6cm. Gọi E là trung điểm AC, tia phân giác của
A
^
cắt BC tại D.a) Tính BC.b) Chứng minh:
∆
B
A
D
∆
E
A
D
.
c) Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh điểm D cách đều AB và AC.
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 3cm, AC = 6cm. Gọi E là trung điểm AC, tia phân giác của A ^ cắt BC tại D.
a) Tính BC.
b) Chứng minh: ∆ B A D = ∆ E A D .
c) Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh điểm D cách đều AB và AC.
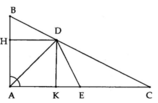

c) Do DH vuông góc với AB nên DH là khoảng cách từ D đến AB.
Tương tự DK là khoảng cách từ D đến AC.
Suy ra DH = DK. Suy ra điểm D cách đều AB và AC.
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=3cm;AC=4cm . Gọi I là trung điểm của BC. Qua M lần lượt kẻ các đường thẳng vuông với AB và AC tại K và H
a) Chứng minh tứ giác AKIH là hình chữ nhật;
b) Lấy điểm D đối xứng vs điểm I qua điểm K. Chứng Minh tứ giác IBDA là hình thoi
a: Xét tứ giác AKIH có
\(\widehat{AKI}=\widehat{AHI}=\widehat{HAK}=90^0\)
Do đó: AKIH là hình chữ nhật
Đúng 0
Bình luận (0)
Cho Tam giác ABC Vuông tại A Biết AB Bằng 3cm,AC4cm, M Là trung điểm của BC Từ M Kẻ MI Vuông Góc với AB tại I MK Vuông Góc Với AC Tại K.a, Tính diện Tích Tam Giác ABC.b,Tứ Giác AIMK Là Hình Gì Vì sao?c, Gọi EF lần luotj là trung điểm của IM Và KM Gọi giao điểm của IK với AE Và AF Lần luotj là H và N Chứng Minh IHKNd,Giả sử tam giác ABC có cạnh BC ko đổi Tam Giác ABC Có thêm điều kiện gì để Diện tích Lớn nhất
Đọc tiếp
Cho Tam giác ABC Vuông tại A Biết AB Bằng 3cm,AC=4cm, M Là trung điểm của BC Từ M Kẻ MI Vuông Góc với AB tại I MK Vuông Góc Với AC Tại K.
a, Tính diện Tích Tam Giác ABC.
b,Tứ Giác AIMK Là Hình Gì Vì sao?
c, Gọi EF lần luotj là trung điểm của IM Và KM Gọi giao điểm của IK với AE Và AF Lần luotj là H và N Chứng Minh IH=KN
d,Giả sử tam giác ABC có cạnh BC ko đổi Tam Giác ABC Có thêm điều kiện gì để Diện tích Lớn nhất
a: \(S=\dfrac{AB\cdot AC}{2}=6\left(cm^2\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, có AB = 3cm, AC= 4cm , AH là đường cao . Điểm D ,E lần lượt đối xứng với H qua AB, AC . TÍNH DE?
= 5 cm nhá bạn yêu dấu ơi, còn cách làm thì để mình tìm cách giải thích cho, cái này mình hơi tệ ![]() , thông cảm, mình tìm cách giải thích cho bạn sau
, thông cảm, mình tìm cách giải thích cho bạn sau
Đúng 0
Bình luận (2)
cho tam giác ABC có BC=4cm. gọi D,E lần lượt là trung điểm của AC,AB M,N lần lượt là trung điểm của BE ,CD
MN cắt BD tại P MN cắt CE tại Q
a) tính MN
b) chứng minh MO=PQ=QN
Ai giúp mình sẽ tick cho 10 like luôn


