Cho bốn số a, b, c, d sao cho ab=1; ac+bd=2. Chứng minh rằng 1-cd không thể là số âm.
GIÚP MÌNH NHANH ĐIIIII><
GẤP LẮM, CHIỀU NỘP RỒI. THANK YOU
1. Cho bốn điểm A, B, C, D sao cho AB//CD và AD//BC. Chứng minh tam giác ABC = tam giác CDA.
2. Cho bốn điểm A, B, C, D sao cho AB//CD và AD//BC. Chứng minh AB = CD.
3. Cho tam giác ABC. Trên các tia đối AB, AC lần lượt lấy các điểm E, F sao cho AE = AC, AF = AC. Chứng minh tam giác ABC = tam giác AFE.
1) Ta có hình vẽ sau:
Vì AB // CD nên \(\widehat{A_1}\) = \(\widehat{C_1}\) (so le trong)
AD // BC nên \(\widehat{A_2}\) = \(\widehat{C_2}\) ( so le trong)
Xét ΔABC và ΔCDA có:
\(\widehat{A_1}\) = \(\widehat{C_1}\) (cm trên)
AC: Cạnh chung
\(\widehat{A_2}\) = \(\widehat{C_2}\) (cm trên)
\(\Rightarrow\) ΔABC = ΔCDA (g.c.g) (đpcm)
2) Chứng minh tương tự ta có: ΔCDA = ABC (g.c.g)
\(\Rightarrow\) AB = CD ( 2 cạnh tương ứng) (đpcm)
3) Mình sửa lại chỗ AE = AC là AE = AB đó nha, bn ghi nhầm đề!!!
Ta có hình vẽ sau:
Xét ΔABC và ΔAFE có:
AE = AB (gt)
\(\widehat{A_1}\) = \(\widehat{A_2}\) (đối đỉnh)
AF = AC (gt)
\(\Rightarrow\) ΔABC = ΔAFE(c.g.c) (đpcm)
Bạn áp dụng trường hợp bằng nhau cạnh - góc - cạnh của tam giác rồi chứng minh nha
1, Bốn điểm A, B, C, D cùng thuộc đường thẳng a sao cho C nằm giữa A và B còn B nằm giữa C và D. Cho biết AB = 5cm, AD = 8cm và BC = 2cm.
a, Chứng tỏ rằng: AC = BD.
b, So sánh hai đoạn thẳng AB và CD.
VẼ HÌNH NỮA NHA
Cho bốn số nguyên thỏa mãn điều kiện: a+b=c+d và ab+1=cd. Chứng minh: c=d
1) Tim so co hai chữ số ab sao cho ab=(a+b)^2 2) Tim so co BỐN chữ số abcd sao cho abcd=(ab+ cd)^2
1, ab= (a+b)x (a+b) <=> a*10+b= a*a+ 2*a*b+ b*b <=> a*10 - a*a - 2*a*b+b- b*b =0 <=> a*( 10 -a - 2 *b) + b*( 1- b) =0 <=> a*( 10 -s- 2*b) =0 và b *(1-b)= 0 vì 10> a>0,10> b>=0 nên a*( 10- a- 2*b)=0 thì 10- a- 2*b =0, b*(1-b) =0 thì b=0 hoặc 1-b=0. với b =0 thì thay vào 10- a- 2*0 =0 <=> a = 10 loại. với 1-b= 0 <=> b=1 thì thay vào 10 - a- 2*1 =0 <=> a= 8 nhận. vây số cần tìm 81.
2, abcd= 2025 (abcd= ab *100 + cd = ab*ab+ ab*cd +ab*cd +cd*cd)
1) Tim so co hai chữ số ab sao cho ab=(a+b)^2
2) Tim so co BỐN chữ số abcd sao cho abcd=(ab+ cd)^2
1,
ab= (a+b)x (a+b) <=> a*10+b= a*a+ 2*a*b+ b*b <=> a*10 - a*a - 2*a*b+b- b*b =0 <=> a*( 10 -a - 2 *b) + b*( 1- b) =0 <=> a*( 10 -s- 2*b) =0 và b *(1-b)= 0 vì 10> a>0,10> b>=0 nên a*( 10- a- 2*b)=0 thì 10- a- 2*b =0, b*(1-b) =0 thì b=0 hoặc 1-b=0. với b =0 thì thay vào 10- a- 2*0 =0 <=> a = 10 loại. với 1-b= 0 <=> b=1 thì thay vào 10 - a- 2*1 =0 <=> a= 8 nhận. vây số cần tìm 81.
2, abcd= 2025 (abcd= ab *100 + cd = ab*ab+ ab*cd +ab*cd +cd*cd)
Cho bốn sô nguyên dương a, b, c, d sao cho: a2+b2=c2+d2 . Chứng tỏ rằng tổng
bốn số a + b + c + d là một hợp số.
Câu hỏi của Lê Linh An - Toán lớp 6 - Học toán với OnlineMath
Em tham khảo nhé!
Xét :\(\left(a^2+b^2+c^2+d^2\right)+\left(a+b+c+d\right)\)
\(=\left(a^2+a\right)+\left(b^2+b\right)+\left(c^2+c\right)+\left(d^2+d\right)\)
\(=a.\left(a+1\right)+b.\left(b+1\right)+c.\left(c+1\right)+d.\left(d+1\right)\)
Ta có : \(a.\left(a+1\right);b.\left(b+1\right);c.\left(c+1\right);d.\left(d+1\right)\) là tích của hai số nguyên dương liên tiếp .Do đó chúng chia hết cho \(2\)
\(\implies\) \(\left(a^2+b^2+c^2+d^2\right)+\left(a+b+c+d\right)\) chia hết cho \(2\)
Mà \(a^2+b^2+c^2+d^2=2.\left(b^2+d^2\right)\) chia hết cho \(2\)
\(\implies\) \(a+b+c+d\) chia hết cho \(2\)
Mà \(a+b+c+d\) \(\geq\) \(4\) \(\implies\) \(a+b+c+d\) là hợp số\(\left(đpcm\right)\)
Cho bốn điểm A, B, C, D thuộc đường tròn (O) sao cho AB = CD. Chứng minh rằng ∠(AOB) = ∠(COD)
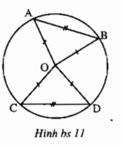
Xét ΔAOB và ΔCOD có:
OA = OC (cùng bằng bán kính đường tròn)
OB = OD (cùng bằng bán kính đường tròn)
AB = CD (gt)
⇒ ΔAOB = ΔCOD (c.c.c)
⇒ ∠AOB = ∠COD (hai góc t.ư)
cho hỏi: có bốn số nguyên a,b,c,d sao cho : 2b=a+c ; 2c=b+d và c^2+d^2
Tìm bốn số nguyên a, b, c, d sao cho
a + b + c + d = 1
a + c + d = 2
a + b + d = 3
a + b + c = 4
ta có:
(a+ b+ c+ d)- ( a+c+d)=b
=>1-2
=> -1
vậy b= -1
điền dần vào các số a, b, c, d ta có
a+(-1)+c+d =1
=>[a+(-1)+c+d]-a+b+c
=> 1-4
=> -3 => d=-3
giờ ta có:a+(-1)+c+(-3)=1
=>[a+(-1)+c+(-3)]-a+b+d=c
=>1-3 => c=-2
còn lại a+ (-1)+(-2)+(-3)=1
=> a=7
tích mk nhé