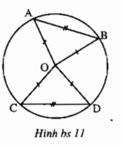
Xét ΔAOB và ΔCOD có:
OA = OC (cùng bằng bán kính đường tròn)
OB = OD (cùng bằng bán kính đường tròn)
AB = CD (gt)
⇒ ΔAOB = ΔCOD (c.c.c)
⇒ ∠AOB = ∠COD (hai góc t.ư)

Xét ΔAOB và ΔCOD có:
OA = OC (cùng bằng bán kính đường tròn)
OB = OD (cùng bằng bán kính đường tròn)
AB = CD (gt)
⇒ ΔAOB = ΔCOD (c.c.c)
⇒ ∠AOB = ∠COD (hai góc t.ư)
Cho bốn điểm A,B,C,D thuộc đường tròn O sao cho AB=CD.CMR\(\widehat{AOB}=\widehat{COD}\)
Cho 4 điểm A,B,C,D thuộc đường tròn (O) sao cho AB = CD . CMR: \(\widehat{AOB}=\widehat{COD}\)
Cho 4 điểm A;B;C:D thuộc đường tròn O,sao cho AB=CD.Chứng minh góc AOB=COD
CHO ĐƯỜNG TRÒN TÂM O ĐƯỜNG KÍNH A,CD THUỘC ĐƯỜNG TRÒN TÂM O SAO CHO C VÀ D NẰM KHÁC PHÍA AB VÀ AC=BD
CHỨNG MINH RẰNG 3 ĐIỂM C,O,D THẲNG HÀNG
MONG CÁC BẠN GIÚP
Cho tam giác AOB. Trên tia đối của tia OA lấy điểm C sao cho OC = OA , trên tia đối của tia OB lấy điểm D sao cho OD = OB
1, chứng ming : ∆AOB = ∆COD
2, gọi M là điểm nằm giữa A và B . Tia MO cắt CD tại N . Chứng minh rằng MB = ND
3,Trên tia AB lấy M , trên tia DC lấy N sao cho BM=DN . CMR: M,O,N thẳng hàng
cho 1 điểm O nằm ngoài đường thẳng xy . Hạ OA vuông góc với xy . Trên tia Ay lấy lần lượt các điểm B,C,D sao cho AB=BC=CD . Chứng minh rằng \(\widehat{AOB}\)>\(\widehat{BOC}\)>\(\widehat{COD}\)
Cho một điểm O ở ngoài đường thẳng xy , hạ OA vuông góc với xy \(\left(A\in xy\right)\). Trên tia Ay lần lượt lấy các điểm B,C,D sao cho AB=BC=CD .
Chửng minh rằng :\(\widehat{AOB}>\widehat{BOC}>\widehat{COD}\)
Trong mặt phẳng, cho đường tròn tâm O. Một đường thẳng cắt đường tròn tại 2 điểm A và B thỏa
mãn AOB=136°.Trên đoạn thẳng AB, ta lấy 2 điểm C và D sao cho AOC=98° và BOD=74°.
Tìm số do của COD.
OA. 18⁰
B. 24°
C. 36°
D. 38°
Cho đường thẳng d và hai điểm A, B thuộc cùng một mặt phẳng bờ d, sao cho đường thẳng AB không vuông góc với d.
a) Vẽ đường tròn tâm O đi qua hai điểm A,B sao cho O nằm trên d;
b) Gọi C, D là giao điểm của d với đường tròn tâm O kể trên. Chứng minh O nằm trên các đường trung trực các đoạn thẳng BC, AD, AC, DB, CD.