Tính :
a) 0,(3) + 0,(45)
b) 3,(45) - 2,9(2)
TH
Những câu hỏi liên quan
Không dùng bảng số và máy tính, chứng minh rằng :
a) sin20^0+2sin40^0-sin100^0sin40^0
b) dfrac{sinleft(45^0+alpharight)-cosleft(45^0+alpharight)}{sinleft(45^0+alpharight)+cosleft(45^0+alpharight)}tanalpha
c) dfrac{3cot^215^0-1}{3-cot^215^0}-cot15^0
d) sin200^0sin310^0+cos340^0cos50^0dfrac{sqrt{3}}{2}
Đọc tiếp
Không dùng bảng số và máy tính, chứng minh rằng :
a) \(\sin20^0+2\sin40^0-\sin100^0=\sin40^0\)
b) \(\dfrac{\sin\left(45^0+\alpha\right)-\cos\left(45^0+\alpha\right)}{\sin\left(45^0+\alpha\right)+\cos\left(45^0+\alpha\right)}=\tan\alpha\)
c) \(\dfrac{3\cot^215^0-1}{3-\cot^215^0}=-\cot15^0\)
d) \(\sin200^0\sin310^0+\cos340^0\cos50^0=\dfrac{\sqrt{3}}{2}\)
a) \(sin20^o+2sin40^o-sin100^o=sin20^o-sin100^o+2sin40^o\)
\(=2cos60^osin\left(-40^o\right)+2sin40^o\)\(=-2cos60^osin40^o+2sin40^o\)
\(=2sin40^o\left(-cos60^o+1\right)=2sin40^o.\left(-\dfrac{1}{2}+1\right)=sin40^o\)(đpcm).
Đúng 0
Bình luận (0)
b) \(\dfrac{sin\left(45^o+\alpha\right)-cos\left(45^o+\alpha\right)}{sin\left(45^o+\alpha\right)+cos\left(45^o+\alpha\right)}\)
\(=\dfrac{sin\left(45^o+\alpha\right)-sin\left(45^o-\alpha\right)}{sin\left(45^o+\alpha\right)+sin\left(45^o-\alpha\right)}=\dfrac{2cos45^o.sin\alpha}{2sin45^o.cos\alpha}\)
\(=tan\alpha\) (Đpcm).
Đúng 0
Bình luận (0)
d) \(sin200^osin310^o+cos340^ocos50^o\)
\(=sin20^o.sin50^o+cos20^ocos50^o\)
\(=cos\left(50^o-20^o\right)=cos30^o\).
Đúng 0
Bình luận (0)
tìm x thuộc z , biêt
a)3x + 45 . 5x - 45 = 0
b) 3x + 45 . 5x - 45 < 0
c) ( x2 + 3 ) . ( 2x - 2016 ) =0
d) 3x + 45 . 5x - 45 >0
e) 3x + 45 . 5x - 45 = -7
Tìm x, biết:
a) (x – 45).27 = 0
b) 45.(2x – 4).13 = 0
c) (x – 3).(x – 5) = 0
a) (x – 45).27 = 0 ó x – 45 = 0 ó x = 45
b) 45.(2x – 4).13 = 0 ó 2x – 4 = 0 ó 2x – 4 = 0 ó 2x = 4 ó x = 2
c) (x – 3).(x – 5) = 0
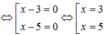
Vậy tập nghiệm của phương trình là S = {3;5}
Đúng 0
Bình luận (0)
Bài 1: Thực hiện phép tính
a) (45-25).(-11)+29.(-3-17)
b) (36-6).(-5)+21.(-17-3)
Bài 2: Tìm x, biết:
a) -4.(2x+9)-(-8x+3)-(x-13)=0 b) 7x.(2+x)-7x.(x+3)=0
Trả lời
Bài 1:
a)(45-25).(-11)+29.(-3-17)
=20.(-11)+29.(-20)
=20.(-11)+(-29).20
=20.[(-11)+(-29)]
=20.(-30)
=-600
b)(36-6).(-5)+21.(-17-3)
=30.(-5)+21.(-20)
=(-150)+(-420)
=-570
Đúng 0
Bình luận (0)
trả lời:
a,(45-25).(-11)+29.(-3-17)
=20.(-11)+29.(-20)
=20.(-11)+(-29).20
=20.[(-11)+(-29).20
=20.(-30)
=-600
học tốt
Đúng 0
Bình luận (0)
Giải giúp mình nha
1)Tìm x:
A)x. ( x^2 - 4 ) = 0
B)( 2x - 3 ) + ( -3x ) - ( x - 5 ) = 40
C)2.( 3 + 6x ) + 8.( x - 5 ) = -52
D)( x^2 - 144 ).( x -5 ).x = 0
E)x^2 - ( 2x + 1 ) - ( 3 - x ) = - ( 5 - x^2 )
2)Tính hợp lý
A)-45.12 + 34.(-45) - 45.54
B)43.( 57 - 33 ) + 33.( 43 - 57 )
Xem chi tiết
Bài 1:
a) Ta có: \(x\left(x^2-4\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{0;2;-2\right\}\)
b) Ta có: \(\left(2x-3\right)+\left(-3x\right)-\left(x-5\right)=40\)
\(\Leftrightarrow2x-3-3x-x+5=40\)
\(\Leftrightarrow-2x+2=40\)
\(\Leftrightarrow-2x=38\)
hay x=-19
Vậy: x=-19
Bài 2:
a) Ta có: \(-45\cdot12+34\cdot\left(-45\right)-45\cdot54\)
\(=-45\cdot\left(12+34+54\right)\)
\(=-45\cdot100\)
\(=-4500\)
b) Ta có: \(43\cdot\left(57-33\right)+33\cdot\left(43-57\right)\)
\(=43\cdot57-43\cdot33+43\cdot33-33\cdot57\)
\(=43\cdot57-33\cdot57\)
\(=57\cdot\left(43-33\right)\)
\(=57\cdot10=570\)
Đúng 1
Bình luận (0)
1.tính
a) 3 -(-2/7)^0 + (1/2)^2 chia 2
b) (5^2) -(-5^2)+ ((-2)^3)^2
C) 2^3 + 3(1/2)^0 - 2^-2 . 4+[(-2)^2 chia 1/2 ] .8
d) 2^2 - 2^3 +2^4 +2^5 +.........+2^44+2^45
Biết rằng (2+x+2x3)15 = a0 + a1x + a2x2 + a3x3 + ... + a45x45
Tính S= a1 + a2 + a3 + .... + a45
Đặt \(A\left(x\right)=\left(2+x+2x^3\right)^{15}=a_0+a_1x+a_2x^2+a_3x^3+...+a_{45}x^{45}\)
Như vậy \(A\left(0\right)=\left(2+0+2.0^3\right)^{15}=a_0+a_1.0+a_2.0^2+a_3.0^3+...+a_{45}.0^{45}=a_0\)
hay \(a_0=\left(2+0+2.0^3\right)^{15}=2^{15}\)
Lại có \(A\left(1\right)=\left(2+1+2.1^3\right)^{15}=a_0+a_1.1+a_2.1^2+a_3.1^3+...+a_{45}.1^{45}\)
\(=a_0+a_1+a_2+a_3+...+a_{45}=a_0+S=2^{15}+S\)
hay \(2^{15}+S=\left(2+1+2.1^3\right)^{15}=5^{15}\)
\(\Rightarrow S=5^{15}-2^{15}\)
Đúng 0
Bình luận (0)
1. tan(2x + 10°) + cotx =0
2. tan(2x + 45°) . tan(180° - x/2) =1
3. cot(3x + 45°) - tan20° =0
tan(2x+10o)+cot(x)=0
<=> tan(2x+10o)+tan(90o-x)=0
<=>tan(x+100o)*[1-tan(2x-10o)*tan(90o-x)]=0
*tan(x+100o)=0 => x=....
*1-tan(2x-10o)*tan(90o-x)=0
<=> tan(2x-10o)=tanx <=> x=....
Đúng 0
Bình luận (0)
rút gọn
a)3 √5 + √20-2 √5
b)2 √2+ √8+ √50
c) 4√3+ √ 27 -√45 +2 √5
d) √ 75+ √ 48- √300
e)( √28- √12- √7) √7 +2 √21
f)( √99- √18- √11) √11+3 √22
g)3 √45-5 √125x +7 √20x+28(x>=0)
a: \(=3\sqrt{5}+2\sqrt{5}-2\sqrt{5}=3\sqrt{5}\)
b: \(=2\sqrt{2}+2\sqrt{2}+5\sqrt{2}=9\sqrt{2}\)
c: \(=4\sqrt{3}+3\sqrt{3}-3\sqrt{5}+2\sqrt{5}=7\sqrt{3}-\sqrt{5}\)
d: \(=5\sqrt{3}+4\sqrt{3}-10\sqrt{3}=-\sqrt{3}\)
e: \(=\left(\sqrt{7}-2\sqrt{3}\right)\cdot\sqrt{7}+2\sqrt{21}\)
=7-2*căn 21+2*căn 21
=7
f: \(=\left(2\sqrt{11}-3\sqrt{2}\right)\cdot\sqrt{11}+3\sqrt{22}\)
=22-3*căn 22+3*căn 22
=22
Đúng 1
Bình luận (1)
a) \(3\sqrt{5}+\sqrt{20}-2\sqrt{5}\)
\(=3\sqrt{5}+2\sqrt{5}-2\sqrt{5}\)
\(=3\sqrt{5}\)
b) \(2\sqrt{2}+\sqrt{8}+\sqrt{50}\)
\(=2\sqrt{2}+2\sqrt{2}+5\sqrt{2}\)
\(=9\sqrt{5}\)
c) \(4\sqrt{3}+\sqrt{27}-\sqrt{45}+2\sqrt{5}\)
\(=4\sqrt{3}+3\sqrt{3}-3\sqrt{5}+2\sqrt{5}\)
\(=7\sqrt{3}-\sqrt{5}\)
d) \(\sqrt{75}+\sqrt{48}-\sqrt{300}\)
\(=5\sqrt{3}+4\sqrt{3}-10\sqrt{3}\)
\(=-\sqrt{3}\)
e) \(\left(\sqrt{28}-\sqrt{12}-\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)
\(=\left(2\sqrt{7}-2\sqrt{3}-\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)
\(=\left(\sqrt{7}-2\sqrt{3}\right)\sqrt{7}+2\sqrt{21}\)
\(=7-2\sqrt{21}+2\sqrt{21}\)
\(=7\)
f) \(\left(\sqrt{99}-\sqrt{18}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)
\(=\left(3\sqrt{11}-3\sqrt{2}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)
\(=\left(2\sqrt{11}-3\sqrt{2}\right)\sqrt{11}+3\sqrt{22}\)
\(=22-3\sqrt{22}+3\sqrt{22}\)
\(=22\)
g) \(3\sqrt{45}-5\sqrt{125x}+7\sqrt{20x}+28\)
\(=9\sqrt{5}-25\sqrt{5x}+14\sqrt{5x}+28\)
\(=9\sqrt{5}-11\sqrt{5x}+28\)
Đúng 1
Bình luận (0)