Giúp mình giải bài này:
Cho \(\Delta ABC\) nhọn nội tiếp (O; R) AB<AC. Các đường cao BE, CF cắt nhau tại H.
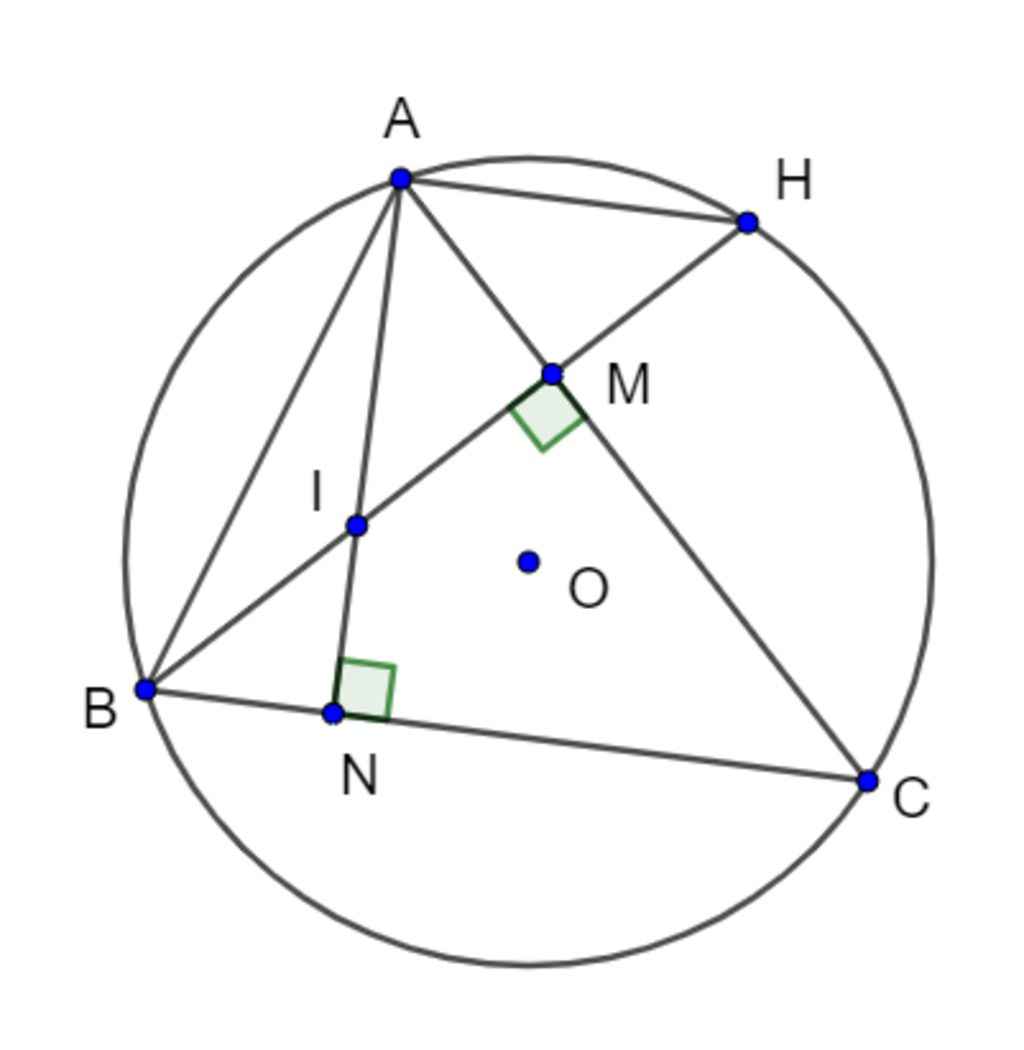
a) Gọi I tâm đường tròn nội tiếp \(\Delta ABC\). Gọi D là giao điểm của của tia AI với (O). Chứng minh \(\Delta BDI\) cân
b) Gọi M, N lần lượt là tiếp điểm của (I) với AB, BC. Kẻ CQ vuông góc với AD tại Q. Chứng minh M, N, Q thẳng hàng.