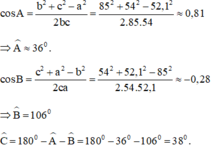Tính các góc của tam giác ABC . Biết rằng Â= 2B̂ = 3C
PT
Những câu hỏi liên quan
Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc Â, B̂, Ĉ.
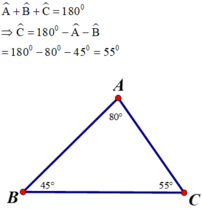
So sánh các cạnh của tam giác ABC, biết rằng: Â = 80º, B̂ = 45º
Theo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
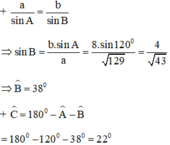
Đúng 0
Bình luận (0)
Bt 1 .tính số đo các góc của tam giác ABC biết Â=2B=3C Tam giác ABC là tam giác gì Bt 2 tính số đo các góc của tam giác MNP bt M=N=4.P Tam giácMNP là tam gì vì sao
Bài 1:
a=2b=3c
=>a/6=b/3=c/2
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{6}=\dfrac{b}{3}=\dfrac{c}{2}=\dfrac{a+b+c}{6+3+2}=\dfrac{180}{11}\)
=>a=1080/11; b=540/11; c=360/11
Đúng 0
Bình luận (0)
Cho tam giác ABC . Phân giác của góc A cắt BC tại D . Tính các góc của tam giác ABC biết ADB = 80 độ và 2B = 3C
a, Tính ba góc của tam giác ABC biết:
6A = 14B = 21C ( góc A , B , C)
b,Tính ba góc của tam giác ABC biết:
A= 3C , B=2C
c, Tính ba góc của tam giác ABC biết:
A=2B ; B= 3C
TẤT CẢ ĐỀU LÀ GÓC NHA
a:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{a}{\dfrac{1}{6}}=\dfrac{b}{\dfrac{1}{14}}=\dfrac{c}{\dfrac{1}{21}}=\dfrac{a+b+c}{\dfrac{1}{6}+\dfrac{1}{14}+\dfrac{1}{21}}=\dfrac{180}{\dfrac{2}{7}}=630\)
Do đó: a=105; b=45; c=30
Đúng 0
Bình luận (0)
Cho tam giác ABC có A = 180°– 3C a) Chứng minh rằng B = 2C. Cho B = 80°, tính số do các góc của tam giác. b) Vẽ tia phân giác của góc B cắt AC tại E. Qua E kẻ đường song song với BC, cắt AB tại D. Chứng minh rằng ED là tia phân giác của góc AEB. Huhu mọi ngừi cố gắng giúp mình nha, thanks nè ❤️❤️❤️
\(a,\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180\) mà \(\widehat{A}=180-3\widehat{C}\)
\(\Rightarrow\widehat{B}+\widehat{C}=180-\widehat{A}=3C\\ \Rightarrow\widehat{B}=2\widehat{C}\)
Thay \(\widehat{B}=80\Rightarrow\widehat{C}=\dfrac{80}{2}=40\Rightarrow\widehat{A}=180-3\cdot40=60\)
\(b,\) Ta có \(DE//BC\)
\(\Rightarrow\widehat{EBC}=\widehat{DEB}\left(SLT\right)\)
Ta có \(\widehat{AEB}=\widehat{C}+\widehat{EBC}=\widehat{C}+\dfrac{1}{2}\widehat{B}=\widehat{C}+\dfrac{1}{2}\cdot2\widehat{C}=2\widehat{C}=\widehat{B}\)
(vì \(\widehat{AEB}\) là góc ngoài \(\Delta EBC\))
\(\Rightarrow\widehat{AED}+\widehat{DEB}=\widehat{ABE}+\widehat{EBC}\)
Mà \(\widehat{EBC}=\widehat{DEB}\left(cmt\right)\)
\(\Rightarrow\widehat{AED}=\widehat{ABE}\)
Mà \(\widehat{EBC}=\widehat{ABE}\left(GT\right)\)
\(\Rightarrow\widehat{DEB}=\widehat{AED}\)
Vậy \(ED\) là phân giác \(\widehat{AEB}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có Â = 120o. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.
Áp dụng định lý côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
= m2 + n2 – 2.m.n.cos120º
= m2 + n2 + mn.
⇒ BC = √( m2 + n2 + mn).
Đúng 0
Bình luận (0)
Cho tam giác ABCvà đường cao AH, H thuộc BC . Biết rằng góc BAHgóc BCA.a) Chứng minh rằng tam giác ABC là tam giác vuông.b) Biết rằng số đo góĉ ABC bằng trung bình cộng của hai góc ̂BACvà góc ACB. Tính số đo các góc của tam giácABC.
Đọc tiếp
Cho tam giác ABCvà đường cao AH, H thuộc BC . Biết rằng góc BAH=góc BCA.
a) Chứng minh rằng tam giác ABC là tam giác vuông.
b) Biết rằng số đo góĉ ABC bằng trung bình cộng của hai góc ̂BACvà góc ACB. Tính số đo các góc của tam giácABC.