-Cho tam giác MNP,có MN=8 cm,NP=10 cm,PM=12 cm.Khi đó,do MN>NP<PM nên góc P<góc M< góc N
NL
Những câu hỏi liên quan
Cho tam giác MNP có \(MN = 6\)cm, \(NP = 8\)cm, \(PM = 7\)cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
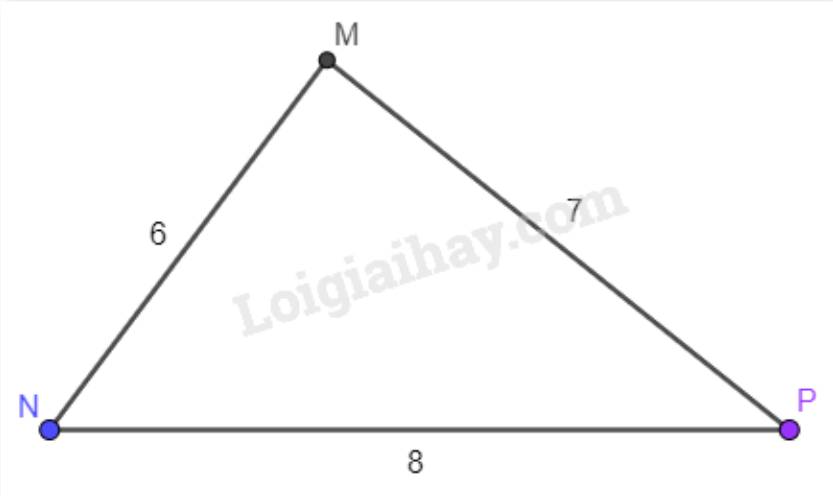
Trong tam giác MNP ta có: \(MN < MP < NP\) (6 < 7 < 8).
Vậy góc lớn nhất trong tam giác MNP là góc M (đối diện với cạnh NP) và góc nhỏ nhất trong tam giác MNP là góc P (đối diện với cạnh MN).
Đúng 0
Bình luận (0)
Cho tam giác MNP có MN=24cm,MA,NB,PC là trung tuyến
a) CM MA+NB>36cm
b) Bỏ giả thiết MN=24cm.CM 3/4(MN+NP+PM)<MA+NB+PC<MN+NP+PM
vẽ tam giác mnp biết MN=2,5 cm,NP=3cm, PM=5cm
Bài này lấy compa ra vẽ nha bạn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác MNP, NP= 6 cm, MN= 10 cm, MP= 8 cm
CMR: tam giác MNR vuông
vẽ hình hộ luôn
Chứng minh tam giác vuông mà thấy số liệu là mừng chết mất =)))
Xét tam giác MNP có:
\(MN^2=NP^2+MP^2\)
\(10^2=6^2+8^2\)
\(100=36+64\)
Vậy trong tam giác này sử dụng được pytago
=> Tam giác MNP vuông tại P
Hình dễ lắm b. Lúc này hình chưa chứng minh là vuông nhé :)
Đúng 0
Bình luận (0)
Bây giờ mới để ý chỗ đề viết sai. Tam giác MNP chứ lấy đâu ra R? :)
Đúng 0
Bình luận (0)
xin lỗi nha chữ P gần chữ v của chữ vuông quá nên mình nhìn nhầm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác MNP vuông tại M có MP = 20 cm MN = 12 cm Tính NP Cần nhanh chóng
Áp dụng PI-ta-go ta có: \(MP^2+MN^2=NP^2\Rightarrow NP=\sqrt{20^2+12^2}=4\sqrt{34}\)cm
Đúng 2
Bình luận (0)
cho tam giác MNP vuông tại M có MN = 6 cm,MP=8 cm .khi đó NP bằng
A. 100cm B.10cm C.14cm D.48cm
Xem thêm câu trả lời
Cho tam giác ABC bằng tam giác MNP. Biết AB+BC=11 cm, MN-NP=3cm. Khi đó MN= ........cm
Cho tam giác ABC bằng tam giác MNP. Biết AB+BC=11 cm, MN-NP= 3 cm. Khi đó MN= 7 cm.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
vẽ vào vở tam giác MNP biết MN=2,5 cm ;NP=3 cm;PM=5cm
b)vẽ vào vở tam giác EFG có EF=FG=GE=3cm sau đó đo ba góc của tam giác EFG rồi cho biết số đo của mỗi góc
Cho tam giác MNP tại M có MN = 3,2 cm MB = 6 cm NP = 6,8 cm a) chứng minh tam giác MNP vuông
b) gọi MK là đường cao. Tính MK , KN, KP( K thuộc NP)
c) tính diện tích tam giác MNP
a, Vì \(NP^2=46,24=10,24+36=MN^2+MP^2\) nên tg MNP vuông tại M
b, Áp dụng HTL: \(\left\{{}\begin{matrix}KN=\dfrac{MN^2}{NP}=\dfrac{128}{85}\left(cm\right)\\KP=\dfrac{MP^2}{NP}=\dfrac{90}{17}\left(cm\right)\\MK=\sqrt{KN\cdot NP}=\dfrac{48}{17}\left(cm\right)\end{matrix}\right.\)
c, \(S_{MNP}=\dfrac{1}{2}MN\cdot MP=\dfrac{1}{2}\cdot6\cdot3,2=9,6\left(cm^2\right)\)
Đúng 3
Bình luận (0)





