Tìm các giá trị của m để phương trình sau có nghiệm và tính các nghiệm ấy theo m:
\(x+|x^2-2x+m|\)
Tìm giá trị của m để phương trình sau có nghiệm và tính các nghiệm ấy theo m : x + \(|x^2-2x+m|=0\)
\(x+\left|x^2-2x+m\right|=0\)
\(\Leftrightarrow\left|x^2-2x+m\right|=-x\)(1)
VÌ VT > 0 nên -x > 0 => x < 0 nên pt ko có nghiệm dương
Từ (1) \(\Rightarrow\orbr{\begin{cases}x^2-2x+m=-x\left(2\right)\\x^2-2x+m=x\left(3\right)\end{cases}}\)
Bây giờ giải 2 và 3 dùng delta sẽ tìm đc x theo m nha
Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.
a ) x 2 − 2 x + m = 0 b ) x 2 + 2 ( m − 1 ) x + m 2 = 0
a) Phương trình x 2 − 2 x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ ' = ( − 1 ) 2 − 1 ⋅ m = 1 − m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et: 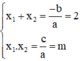
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
b) Phương trình
x 2 + 2 ( m − 1 ) x + m 2 = 0 C ó ( a = 1 ; b = 2 ( m − 1 ) c = m 2 nên b ' = m − 1 ⇒ Δ ' = b ' 2 − a c = ( m − 1 ) 2 − m 2 = − 2 m + 1
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et: 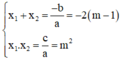
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m 2
Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.
x2 + 2(m – 1)x + m2 = 0
Phương trình x2 + 2(m – 1)x + m2 = 0
Có a = 1; b = 2(m – 1); c = m2 nên b’ = m-1
⇒ Δ’ = b'2 – ac = (m – 1)2 – m2 = - 2m + 1.
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et: 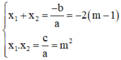
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m2
Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.
x2 – 2x + m = 0;
Phương trình x2 – 2x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ’ = (-1)2 – 1.m = 1 – m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et: 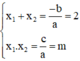
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
Các bạn giúp mình giải mấy bài toán khó lớp 9 này với! Thank nhiều!?
1)Viết đa thức f(x)= 3x^2-2x+4 theo lũy thừa giảm dần của (x-1) 2)Cho phương trình: x^2-2(m+1)x-3m^2 -2m-1=0 a- Chứng minh rằng: phương trình luôn có 2 nghiệm trái dấu với mọi giá trị của m b- Tìm các giá trị của m để phương trình có nghiệm x=-1 c- Tìm các giá trị của m để phương trình có 2 nghiệm x1,x2 thỏa... hiển thị thêm
cho pt \(mx^2-2mx+1=0\)
a) Tìm các giá trị của m để phương trình có nghiệm và tính nghiệm của phương trình theo m
b) Tìm các giá trị của m để phương trình có 2 nghiệm sao cho 1 nghiệm gấp đôi nghiệm kia
a)
+) Với m = 0 thay vào phương trình ta có: 1 = 0 => loại
+) Với m khác 0
\(\Delta'=m^2-m=m\left(m-1\right)\)
Để phương trình có nghiệm điều kiện là: \(m\left(m-1\right)\ge0\)
TH1: m \(\ge\)0 và m - 1 \(\ge\)0
<=> m \(\ge\) 0 và m \(\ge\)1
<=> m \(\ge\)1
TH2: m \(\le\) 0 và m - 1 \(\le\)0
<=> m \(\le\)0 và m \(\le\)1
<=> m \(\le\)0
Đối chiếu điều kiên m khác 0
Vậy m < 0 hoặc m \(\ge\)1
+) Tính nghiệm của phương trình theo m. Tự làm áp dụng công thức
b) Gọi \(x_1;x_2\) là hai nghiệm của phương trình
Theo định lí vi ét ta có:
\(x_1x_2=\frac{1}{m};x_1+x_2=\frac{2m}{m}=2\)
Không mất tính tổng quát ta g/s: \(x_1=2x_2\)
=> \(3x_2=2\Leftrightarrow x_2=\frac{2}{3}\)=> \(x_1=\frac{4}{3}\)
Ta có: \(\frac{4}{3}.\frac{2}{3}=\frac{1}{m}\)
<=> \(m=\frac{9}{8}\)( thỏa mãn a )
Thử lại thỏa mãn
Vậy m = 9/8
Cho phương trình ẩn x sau:
(2x+m)(x+1)-2x^2+mx+m-2+0 .tìm các giá trị của m để phương trình có nghiệm không âm
\(\left(2x+m\right)\left(x-1\right)-2x^2+mx+m-2=0\)
\(\Leftrightarrow2x^2-2x+mx-m-2x^2+mx+m-2=0\)
\(\Leftrightarrow2\left(m-1\right)x=2\)
\(\Leftrightarrow x=\frac{2}{m-1}\)
Vì \(2>0\)
\(\Rightarrow m-1>0\)
\(\Rightarrow m>1\)
a) Tìm các giá trị của m để phương trình 2x2-(4m+3)x+2m-1=0 có 2 nghiệm phân biệt.
b) Tính tổng và tích 2 nghiệm theo m.
a) Để phương trình có 2 nghiệm phân biệt
<=> \(\Delta=\left[-\left(4m+3\right)^2\right]-4.2.\left(2m-1\right)=16m^2+24m+9-16m+8=16m^2+8m+1+16=\left(4m+1\right)^2+16>0\)
với mọi giá trị của m.
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
b) Vì phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m nên ta có: x1+x2= \(\dfrac{4m+3}{2}\)và x1.x2=\(\dfrac{2m-1}{2}\)
Đối với mỗi phương trình sau, hãy tìm các giá trị của m để phương trình có nghiệm; tính nghiệm của phương trình theo m :
a) \(mx^2+\left(2m-1\right)x+m+2=0\)
b) \(2x^2-\left(4m+3\right)x+2m^2-1=0\)