cho tam giác ABC vuông ở A, (A;AH), tiếp tuyến BD, CE với đường tròn A
a, cm A, D, E thẳng hàng
b, cm BDE là tam giác cân
c, DE là tt (O). Tứ giác MONE là hình gì
FA
Những câu hỏi liên quan
Bài 4: Cho tam giác ABC vuông cân tại A, BC2cm. Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E.
a) Chứng minh rằng EC vuông góc với BC
b) Tính số đo các góc của tứ giác ABCE.
Bài 5: Cho tam giác ABC vuông ở A, AH là đường cao, M là một điểm trên BC sao cho CMCA. Đường thẳng đi qua M song song với CA cắt AB tại I.
a) Chứng minh AM là phân giác của góc BAH
b) Chứng minh rằng luôn luôn có AB+AC AH+BC
Mình đang cần gấp bài này. Các bạn giúp mình nhé cảm ơn các bạn nhiều.
Đọc tiếp
Bài 4: Cho tam giác ABC vuông cân tại A, BC=2cm. Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E.
a) Chứng minh rằng EC vuông góc với BC
b) Tính số đo các góc của tứ giác ABCE.
Bài 5: Cho tam giác ABC vuông ở A, AH là đường cao, M là một điểm trên BC sao cho CM=CA. Đường thẳng đi qua M song song với CA cắt AB tại I.
a) Chứng minh AM là phân giác của góc BAH
b) Chứng minh rằng luôn luôn có AB+AC< AH+BC
Mình đang cần gấp bài này. Các bạn giúp mình nhé cảm ơn các bạn nhiều.
Bài 4:
a) Ta có tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc CAE + góc BAC = 90 độ, tức là EC vuông góc với BC.
b) Vì tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc BAE = góc BAC + góc CAE = 45 độ + 45 độ = 90 độ. Do đó, tứ giác ABCE là tứ giác vuông.
Bài 5:
a) Gọi K là giao điểm của đường thẳng AM và BH. Ta cần chứng minh góc BAK = góc CAK.
Vì CM = CA, ta có góc CMA = góc CAM. Vì đường thẳng AM song song với CA, nên góc CMA = góc KAB (do AB cắt đường thẳng AM tại I). Từ đó suy ra góc CAM = góc KAB.
Vì AH là đường cao, nên góc BAH = góc CAH. Từ đó suy ra góc BAK = góc CAK.
Vậy, AM là phân giác của góc BAH.
b) Ta có AB + AC = AB + AH + HC = BH + HC > BC (theo bất đẳng thức tam giác).
Vậy, luôn luôn có AB + AC < AH + BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A và tam giác DEF vuông ở D có AB = DE và góc ABC = góc DEF. Chứng minh tam giác ABC = tam giác DEF.
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
Đúng 0
Bình luận (0)
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
Cho tam giác ABC vuông ở A. Đường phân giác A cắt cạnh BC ở D. Qua D kẻ đường thẳng vuông góc với BC cắt AC ở E
a) So sánh: tam giác ABC và tam giác DEC
b) CM: BD=DE ?
a: Xét ΔABC vuông tại A và ΔDEC vuông tại D có
góc C chung
=>ΔABC đồng dạng với ΔDEC
b: góc EDB+góc EAB=180 độ
=>EABD nội tiếp
góc DEB=góc DAB
góc DBE=góc DAC
=>góc DEB=góc DBE
=>DB=DE
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A và có BC=2AB=2a;a=17.56cm. Ở phía ngoài tam giác ABC vẽ hình vuông BCDEl, tam giác đều ABF và ACG. tính diện tích các tam giác AGF và BEF.
tim abf: 17.56:2=?
đề thíu
Đúng 0
Bình luận (0)
thiếu cái gì?
cái này chỉ là 1 phần trong bài, mấy phần kia biết làm rồi
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A. Kẻ AH vuông góc với BC, lấy D trên cạnh BC sao cho BD BACho tam giác ABC vuông ở A. Kẻ AH vuông góc với BC, lấy D trên cạnh BC sao cho BD BAa) tam giác ABD là tam giác gì? Vì sao?b) chứng minh AD là tia phân giác của góc CAH.c) gọi E là hình chiếu của D trên AC. Chứng minh AD là đường trung trực của đoạn thẳng HE.
Đọc tiếp
Cho tam giác ABC vuông ở A. Kẻ AH vuông góc với BC, lấy D trên cạnh BC sao cho BD = BACho tam giác ABC vuông ở A. Kẻ AH vuông góc với BC, lấy D trên cạnh BC sao cho BD = BA
a) tam giác ABD là tam giác gì? Vì sao?
b) chứng minh AD là tia phân giác của góc CAH.
c) gọi E là hình chiếu của D trên AC. Chứng minh AD là đường trung trực của đoạn thẳng HE.
a) tam giác ABD là tam giác gì? Vì sao?
b) chứng minh AD là tia phân giác của góc CAH.
c) gọi E là hình chiếu của D trên AC. Chứng minh AD là đường trung trực của đoạn thẳng HE.
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tai B
b: góc CAD+góc BAD=90 độ
góc HAD+góc BDA=90 độ
mà góc BAD=góc BDA
nên góc CAD=góc HAD
=>ĐPCM
c: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
góc HAD=góc EAD
=>ΔAHD=ΔAED
=>AH=AE; DH=DE
=>AD là trung trực của HE
Đúng 0
Bình luận (0)
Giúp 4 bài này với
Bài 1:Cho tam giác ABC vuông tại A.Đường cao AH. Chứng minh a)B=CAH b)C=CAH
Bài 2:Cho tam giác ABC vuông ở A. Tia phân giác BM,CN của góc B và góc C cắt nhau ở I.Tính BIC
Bài 3: Cho tam giác ABC, A=90độ,AH vuông với BC.Tia phân giác BAH và C cắt nhau ở K. Cm AK vuông góc với CK
Bài 4:Cho tam giác ABC, Điểm M ở miền trong tam giác ABC.Chứng minh BMC > BAC
cho tam giác ABC vuông tại A,ở phía ngoài tam giác ABC vẽ tam giác DBC vuông cân tại D.CMR: AD là duwof phân giác của góc A
Cho tam giác ABC vuông cân ở A , BC=2cm.Vẽ ra phía ngoài của tam giác ABC 1 tam giác ACE vuông cân ở E
a,Tứ giác AECb là hình gì
b,tính các cạnh của tứ giác đó
a) Ta có : ACB = 45° ( ∆ABC vuông cân tại A )
Ta có : AEC = 45° ( ∆ACE vuông cân tại E )
=> ACB = AEC = 45°
Mà 2 góc này ở vị trí so le trong
=> AE//BC
=> AEBC là hình thang
Mà AEC = 90°
=> AEBC là hình thang vuông
Đúng 0
Bình luận (0)
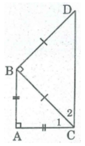
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?
Vì ΔABC vuông cân tại A nên 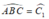
Lại có: 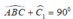 ( tính chất tam giác vuông).
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên 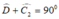
Lại có: ![]() ( tính chất tam giác vuông).
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A . Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B . Tứ giác ABDC là hình gì? Chứng minh
ΔBDC vuông cân tại B
=>góc BCD=góc BDC=45 độ
ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc ABC=góc DCB
mà hai góc này ở vị trí so le trong
nên AB//DC
mà AB vuông góc AC
nên DC vuông góc AC
Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
Do đó: ABDC là hình thang vuông
Đúng 0
Bình luận (0)



