cho tam giác vuông ở A ,cạnh góc vuông AB =2AC. Gọi AH là đường cao của tam giác ABC. CMR BH=4HC
NT
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Cạnh BC=2AC. Gọi AH lầ đường cao của tam giác ABC. CMR: BH=4HC
Cho tam giác vuông ở A ,cạnh góc vuông AB =2AC. Gọi AH là đường cao của tam giác ABC.
-Chứng minh rằng: BH=4HC
helppp
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\dfrac{BH}{CH}=\left(\dfrac{AB}{AC}\right)^2=2^2=4\)
hay BH=4HC
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a đường cao ah gọi i, k lần lượt là trung điểm của hai cạnh ah và bh.
a) cmr: tam giác ahk đồng dạng với tam giác chi
b) CMR: ak vuông góc với ci
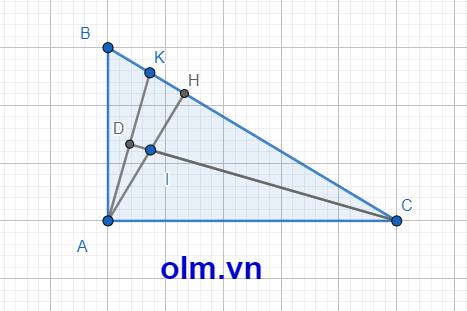
Xét \(\Delta\) HBA và \(\Delta\) ABC có \(\widehat{H}\) = \(\widehat{A}\) = 900; \(\widehat{B}\) chung
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) ABC (g-g)
Tương tự ta có: \(\Delta\) HAC \(\sim\) \(\Delta\) ABC (g-g-g)
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) HAC ( t/c hai tam giác đồng dạng)
⇒ \(\dfrac{HB}{HA}\) = \(\dfrac{HA}{HC}\) = \(\dfrac{BA}{AC}\)( theo khái niệm của tam giác đồng dạng.)
Mặt khác: KI là đường trung bình của tam giác ABH nên:
\(\dfrac{HI}{HA}\) = \(\dfrac{HK}{HB}\) ⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HB}{HA}\)
⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HA}{HC}\) mà \(\widehat{AHK}\) = \(\widehat{CHI}\) = 900
⇒ \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ( c-g-c)
b, Kéo dài CI cắt AK tại D ta có:
vì \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ⇒ \(\widehat{HAK}\) = \(\widehat{HCI}\)
Xét \(\Delta\) HAK và \(\Delta\) DCK có: \(\widehat{A}\) = \(\widehat{C}\) ( cmt)
\(\widehat{K}\) chung
⇒ \(\Delta\) HAK \(\sim\) \(\Delta\) DCK ( g-g)
⇒ \(\widehat{H}\) = \(\widehat{D}\)= 900 ⇒ AK \(\perp\) CI tại D ( đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A cạnh AB = 5cm AC=12 . Từ trung điểm Mcủa cạnh huyền BC Kẻ vuông góc với BC cách cạnh góc vuông tại N
a) Tính MN
b) gọi AH là đường cao của tam giác abc .Tính AH , BH , CH
Mik gọi như này nhé, từ trung điểm M của BC, kẻ vuông góc với BC cắt AC tại N và AB tại K.
Bài làm
a) Xét tam giác ABC vuông tại A có:
\(BC=\sqrt{AB^2+AC^2}\)
hay \(BC=\sqrt{5^2+12^2}=\sqrt{25+144}\)
=> \(BC=\sqrt{169}=13\left(cm\right)\)
=> \(BM=MC=\frac{BC}{2}=\frac{13}{2}=6,5\left(cm\right)\)
Xét tam giác ABC và tam giác MNC có:
\(\widehat{BAC}=\widehat{NMC}=90^0\)
\(\widehat{C}\)chung
=> Tam giác ABC ~ tam giác MNC ( g-g )
=> \(\frac{AB}{MN}=\frac{AC}{MC}\)
hay \(\frac{5}{MN}=\frac{12}{6,5}\Rightarrow MN=\frac{65}{24}\left(cm\right)\)
b) Xét tam giác ABC vuông tại A
Đường cao AH
=> \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
hay \(\frac{1}{AH^2}=\frac{1}{5^2}+\frac{1}{12^2}\)
=> \(\frac{1}{AH^2}=\frac{1}{25}+\frac{1}{144}\)
=> \(\frac{1}{AH^2}=\frac{169}{3600}\)
=> \(AH^2=\frac{3600}{169}\)
=> \(AH=\sqrt{\frac{3600}{169}}=\frac{60}{13}\)( cm )
Xét tam giác AHB vuông tại H có:
Theo Pytago có:
\(BH^2=AB^2-AH^2\)
hay \(BH^2=5^2-\frac{3600}{169}\)
=> \(BH^2=25-\frac{3600}{169}\)
=>\(BH^2=\frac{625}{169}\)
=> \(BH=\frac{25}{13}\)( cm )
Ta có: BH + HC = BC
hay \(\frac{25}{13}+HC=13\)
=> \(HC=13-\frac{25}{13}\)
=> \(HC=\frac{144}{13}\)
Cho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH CEHCho tam giác ABC vuông tại A có đường cao AH. Tia...
Đọc tiếp
Cho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEH. AB>AC
1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A=90 đường cao AH Kẻ HD vuông góc vs AB , HE vuông góc vs AC Gọi O là giao điểm của AH và DE
a) gọi P,Q lần lượt là trung điểm của BH và CH. CMR: DEQP là hình thang vuông
b) CMR O là trực tâm của tam giác ABQ
c) CMR S(ABC) = 2 S(DEQP)
cho tam giác abc vuông tại a đường cao ah , biết ab=15cm , ac=20cm a) cm tam giác hba đồng dạng tam giác abc . tam giác hac đồng dạng tam giác abc . b)tính ah,bh,ch . c) gọi bd là tia phân giác của góc abc . tính ad,dc . d)gọi e,f là chân đường vuông góc kẻ từ h xuống ad và ac . tứ giác aehf là hình gì . e)chứng minh ae.ab=af.ac
Vẽ dùm mình cái hình và phần e
a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
Đúng 0
Bình luận (0)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{15^2}+\dfrac{1}{20^2}=\dfrac{625}{90000}\)
\(\Leftrightarrow AH=12\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow BH^2=15^2-12^2=81\)
hay BH=9(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=AC^2-AH^2=20^2-12^2=256\)
hay CH=16(cm)
Đúng 0
Bình luận (0)
c) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{AD}{15}=\dfrac{CD}{25}=\dfrac{AD+CD}{15+25}=\dfrac{20}{40}=\dfrac{1}{2}\)
Do đó: AD=7,5cm; CD=12,5cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A (AB <AC).đường cao AH . Trên cạnh BC lấy điểm M sao cho BM = BA. TỪ Mker MN vuông góc với AC (N thuộc AC).CMR
a, tam giác ANH cân
b, BC +AH > AB + AC
c, 2AC2 - BC2 = CH2 -BH2
Cho tam giác ABC vuông tại A có AB<AC, đường cao AH. Trên BC lấy M sao cho BA = BM. Từ M kẻ MN vuông góc với AC tại N. CMR:
a) Tam giác ANH cân
b) BC + AH < AB + AC.
c) 2AC^2 - BC^2 = CH^2 - BH^2

