giúp em vớii :33 e cảm ơn ạ ><
CH
Những câu hỏi liên quan
 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80
Đúng 0
Bình luận (0)
Giúp tớ vớii, tớ cảm ơn trc ạ
Bài 14:
a) xx' // yy' vì :
Góc x'An = góc ABy = 60 độ ( 2 góc so le trong)
=> xx' // yy'
b) Ax // By vì:
Góc zBy = góc zAx = 50 độ ( 2 góc đồng vị )
=> Ax // By
Đúng 2
Bình luận (0)
giúp e với ạ e đang cần gấp e cảm ơn anh chị nhiều ạ <33

a: Xét tứ giác MIPC có
K là trung điểm của MP
K là trung điểm của IC
Do đó: MIPC là hình bình hành
mà MI=PI
nên MIPC là hình thoi
Đúng 1
Bình luận (0)
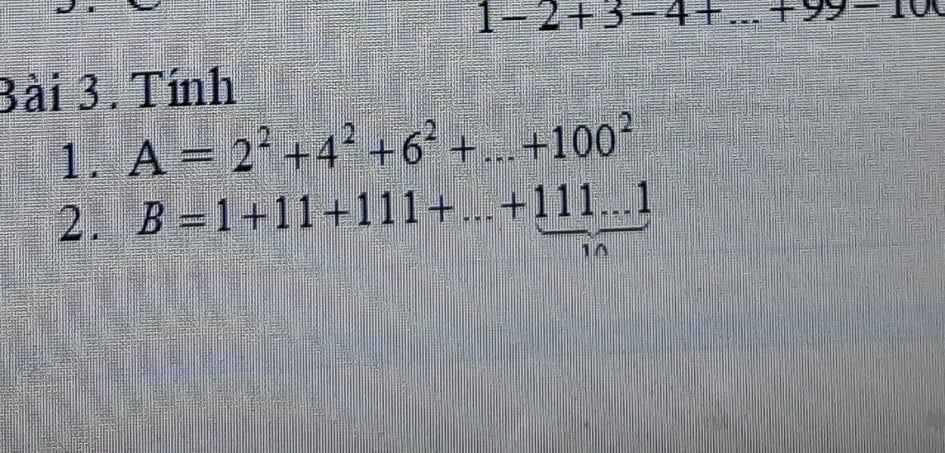 mng giúp em câu a với ạ <33 em cảm ơn
mng giúp em câu a với ạ <33 em cảm ơn
Giúp e với ạ :
1) √(2x+5) ^2 = 5
2) √(-x+2) ^2 = 3
3) √(-2x+1) ^2 = 1 E cảm ơn nhiều ạ
1:
=>|2x+5|=5
=>2x+5=5 hoặc 2x+5=-5
=>x=0 hoặc x=-5
2: =>|x-2|=3
=>x-2=3 hoặc x-2=-3
=>x=-1 hoặc x=5
3: =>|2x-1|=1
=>2x-1=1 hoặc 2x-1=-1
=>x=0 hoặc x=1
Đúng 0
Bình luận (0)
mn giúp em hai bài này vs ạ em cảm ơn nhìuuu:33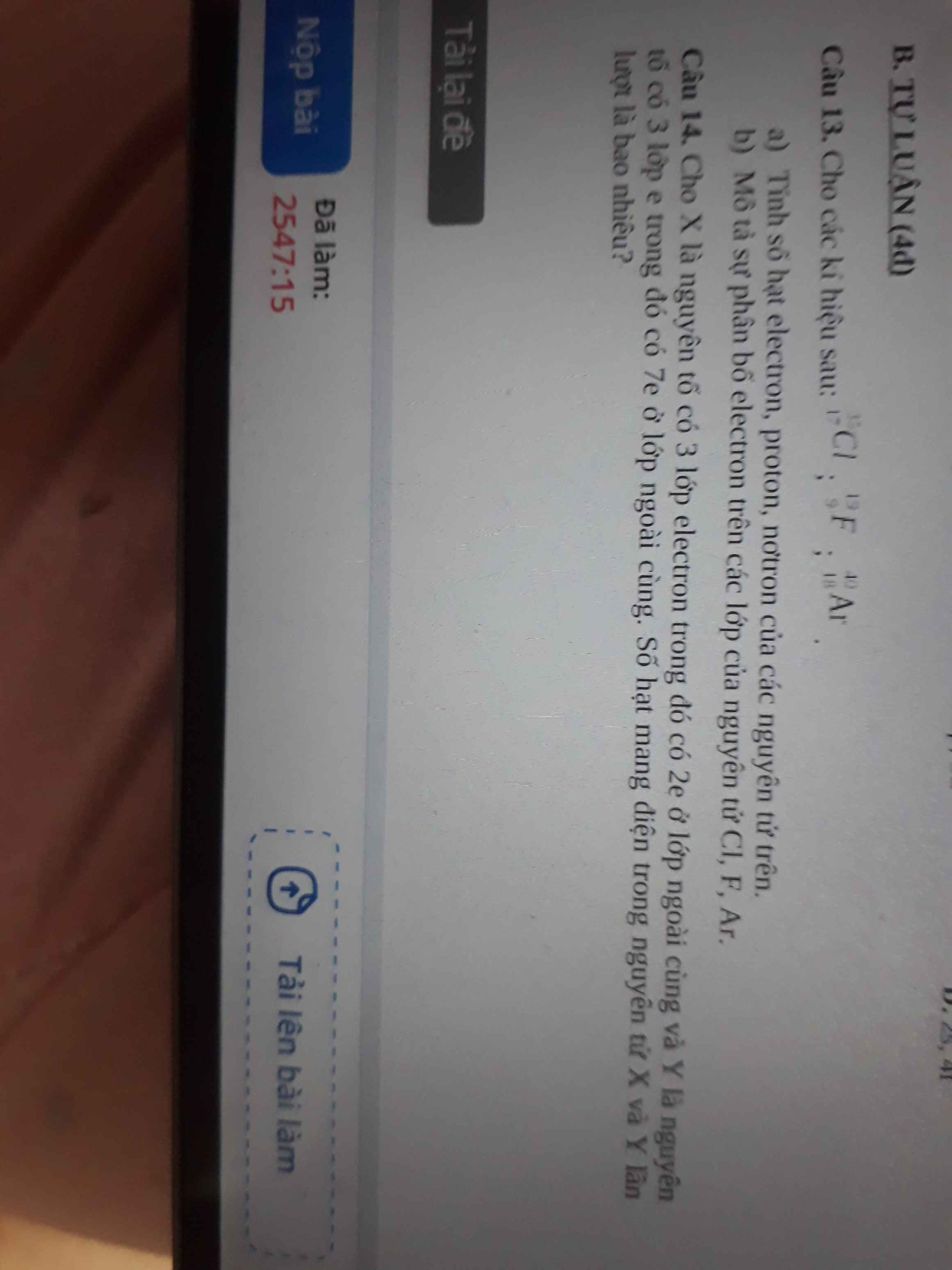
(x+1)+(x+2)+...+(x+30)=750
mong các ac trả lời giúp e ạ
e cảm ơn ac rất nhiều ạ : 33
\(\left(x+1\right)+\left(x+2\right)+\left(x+3\right)+...+\left(x+30\right)=750\)
\(\Rightarrow x+1+x+2+x+3+...+x+30=750\)
Áp dụng tính chất giao hoán các tổng, ta được:
\(\left(1+2+3+...+30\right)+\left(x+x+x+...+x\right)=750\)
Để tính được số phần tử \(x\) xuất hiện, ta sử dụng công thức.
\(P=\dfrac{\left(\text{số đầu - số cuối}\right)}{\text{khoảng cách}}+1=\dfrac{30-1}{1}+1=30\)
Vậy:
\(\left(1+2+3+...+30\right)+30x=750\)
Để tính tổng của dãy số có quy luật, ta sử dụng công thức:
\(T=\left(\dfrac{\text{số đầu - số cuối}}{\text{khoảng cách}}+1\right):2\cdot\left(\text{số đầu + số cuối}\right)\)
\(T=\left(\dfrac{30-1}{1}+1\right):2\cdot\left(30+1\right)\)
\(T=15\cdot31=465\)
Vậy ta được biểu thức rút gọn như sau:
\(465+30x=720\)
\(30x=720-465=255\)
\(x=255:30=8,5\)
Đúng 2
Bình luận (0)

Giúp em với ạ vẽ hình nữa làm mình câu a) cũng được ạ em cảm ơn nhìu ::)>>33
a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)
Đúng 2
Bình luận (0)
Giúp e vs ạ , e đang cần gấp ,em cảm ơn ạ




