Cho tam giác ABC có ABC = 70 độ;ACB = 30 độ . Trên nửa mặt phẳng bờ AC,
không chứa B vẽ đường thẳng thẳng AD song song với BC. Tính số đo các góc A1 và 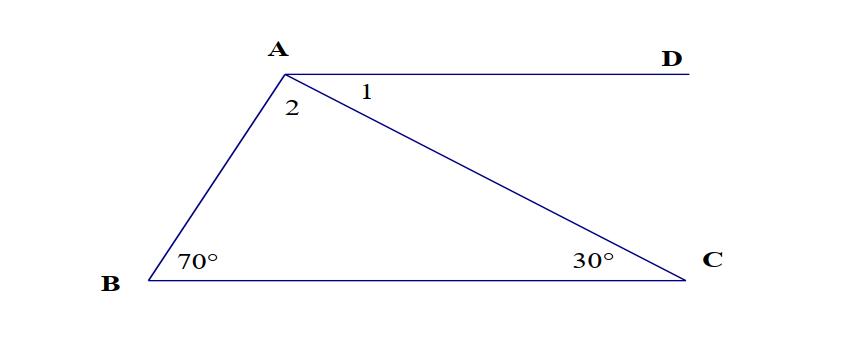 A2.
A2.
H24
Những câu hỏi liên quan
cho tam giác abc có góc a bằng 70 độ góc b bằng 55 độ tam giác abc có phải tam giác cân không vì sao
tam giác ABC tam giác cân vì có góc b và góc c bằng nhau vì a+b+c=180 độ
=> c=180-55-70=55
=>b=c
Đúng 0
Bình luận (0)
\(\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-70^0-55^0=55^0\)
Ta thấy \(\widehat{B}=\widehat{C}\left(=55^0\right)\)
Nên tam giác ABC cân tại A
Đúng 0
Bình luận (0)
tam giác đó là tam giác cân vì
góc c=180-55-70=55 độ
tam giác cân là tam giác có 2 góc ở đáy bằng nhau và 2 cạnh bên bằng nhau
mà tam giác abc có 2 góc ở đáy bằng nhau (55=55)
Đúng 0
Bình luận (0)
cho hai tam giác ABC , DEF có góc A=50 độ , góc E=70 độ , góc F=60 độ , AB=DE , AC=DE . Chứng minh : tam giác ABC=tam giác DEF
\(\widehat{D}=180^0-\widehat{E}-\widehat{F}=50^0=\widehat{A}\\ \left\{{}\begin{matrix}AB=DE\\\widehat{A}=\widehat{D}\\AC=DE\end{matrix}\right.\Rightarrow\Delta ABC=\Delta DEF\left(c.g.c\right)\)
Đúng 2
Bình luận (0)
cho tam giác ABC cân tại A có góc B = 70 độ. Số đo các góc của tam giác ABC
Vì tam giác ABC cân A nên góc B = góc C = 70
Góc A + góc B + góc C = 180° ( tổng 3 góc trong tam giác)
=> Góc A = 180 - 70 x 2 = 40°
Đúng 2
Bình luận (0)
a) cho tam giác ABC có góc A = 80 độ . tam giác ABC là tam giác gì ?
b) cho tam giác ABC cân tại A biết góc A = 70 độ . tinh số đo các góc còn laị của tam giác ABC
* Theo mình thì phần a) Góc A = 90 độ sẽ hợp lý hơn chứ. Vậy nên mình sẽ làm theo cả hai góc A 90 độ và 80 độ nhé ( Nhưng bài của mình phần b) sẽ theo góc A = 90 độ )
a)
Góc A = 80 độ thì sẽ có thể tam giác ABC là tam giác cân, tam giác ⊥ tại B hoặc C, tam giác ABC là tam giác tù hoặc tam giác nhọn
Góc A = 90 độ thì tam giác ABC là tam giác vuông tại A
b)
Theo phần a), ta có: Tam giác ABC cân tại A
=> Góc B = góc C = ( 180 độ - 70 độ ) : 2 = 55 độ
Cho 2 tam giác ABC, tam giác DEF có góc A = 50 độ , góc E = 70 độ , góc F= 60 độ ,AB=DE,AC=DF. Chứng minh tam giác ABC=tam giác DEF
Xét t/giác DEF có \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\) (tổng 3 góc của 1 t/giác)
=> \(\widehat{D}=180^0-\widehat{E}-\widehat{F}=180^0-70^0-60^0=50^0\)
Xét t/giác ABC và t/giác DEF
có: AB = DE (gt)
AC = DF (gt)
\(\widehat{A}=\widehat{D}=50^0\)
=> t/giác ABC = t/giác DEF (c.g.c)
Cho 2 tam giác ABC, tam giác DEF có góc A = 50 độ , góc E = 70 độ , góc F= 60 độ ,AB=DE,AC=DF. Chứng minh tam giác ABC=tam giác DEF
mình cần gấp ạ
cho tam giác abc có số đo góc a là 70 độ số đo góc b là 50 độ hãy so sánh các cạnh của tam giác abc
Vì tổng 3 góc của tam giác luôn bằng 1800 nên góc C là
1800-700-500=600
Theo quan hệ giữa góc và cạnh đối diện:
Vì\(\widehat{A}>\widehat{B}>\widehat{C}\) nên cạnh AC>BC>AB
Đúng 0
Bình luận (0)
Vì tổng 3 góc của tam giác luôn bằng 1800 nên góc C là
1800-700-500=600
Theo quan hệ giữa góc và cạnh đối diện:
VìˆA>ˆB>ˆCA^>B^>C^ nên cạnh AC>BC>AB
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có \(\widehat{BAC}\) = 70 độ. Điểm D nằm trong tam giác ABC sao cho DA = DB và \(\widehat{CAD}\) = 65 độ. Tính \(\widehat{BCD}\)
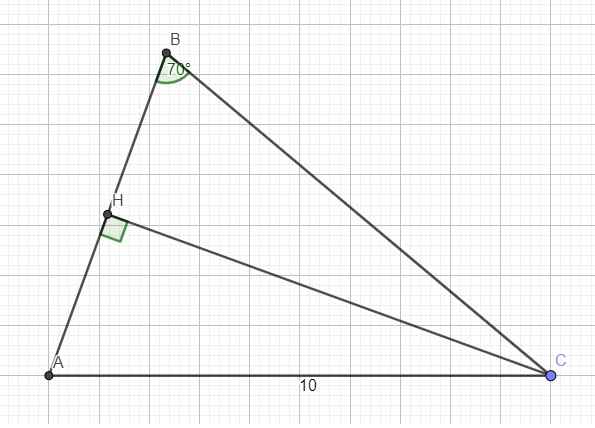
Cho tam giác ABC có AC = 10cm , góc C = 40 độ , góc B = 70 độ.
a. Tính AB , BC
b. Tính diện tích tam giác ABC
Cho tam giác ABC có AC = 10cm , góc C = 40 độ , góc B = 70 độ.
a. Tính AB , BC
b. Tính diện tích tam giác ABC
\(A=180^0-\left(B+C\right)=70^0\)
\(\Rightarrow A=B\Rightarrow\Delta ABC\) cân tại C
\(\Rightarrow BC=AC=10\left(cm\right)\)
Kẻ đường cao CH \(\Rightarrow\) H đồng thời là trung điểm AB
Trong tam giác vuông ACH:
\(cosA=\dfrac{AH}{AC}\Rightarrow AH=AC.cosA=10.cos70^0\approx3,42\left(cm\right)\)
\(AB=2AH\approx6,84\left(cm\right)\)
b. Cũng trong tam giác vuông ACH:
\(sinA=\dfrac{CH}{AC}\Rightarrow CH=AC.sinA=10.sin70^0\approx9,4\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}CH.AB\approx32,15\left(cm^2\right)\)
Đúng 1
Bình luận (0)