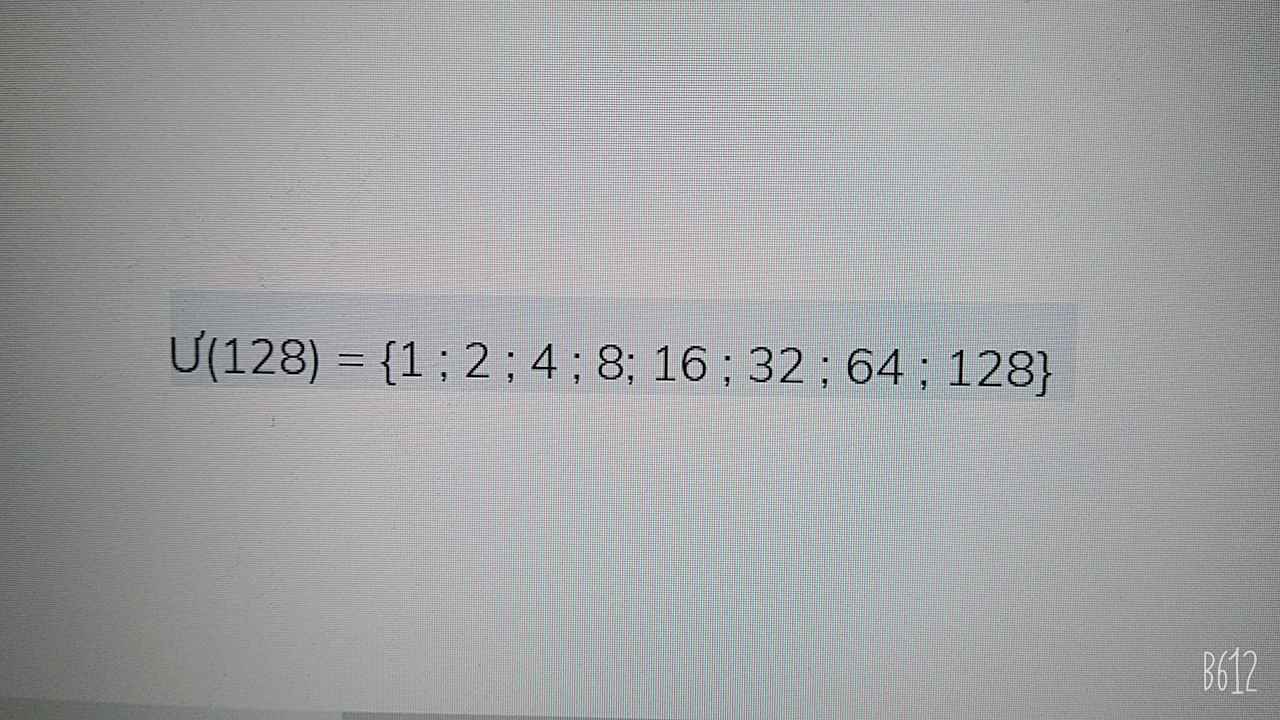
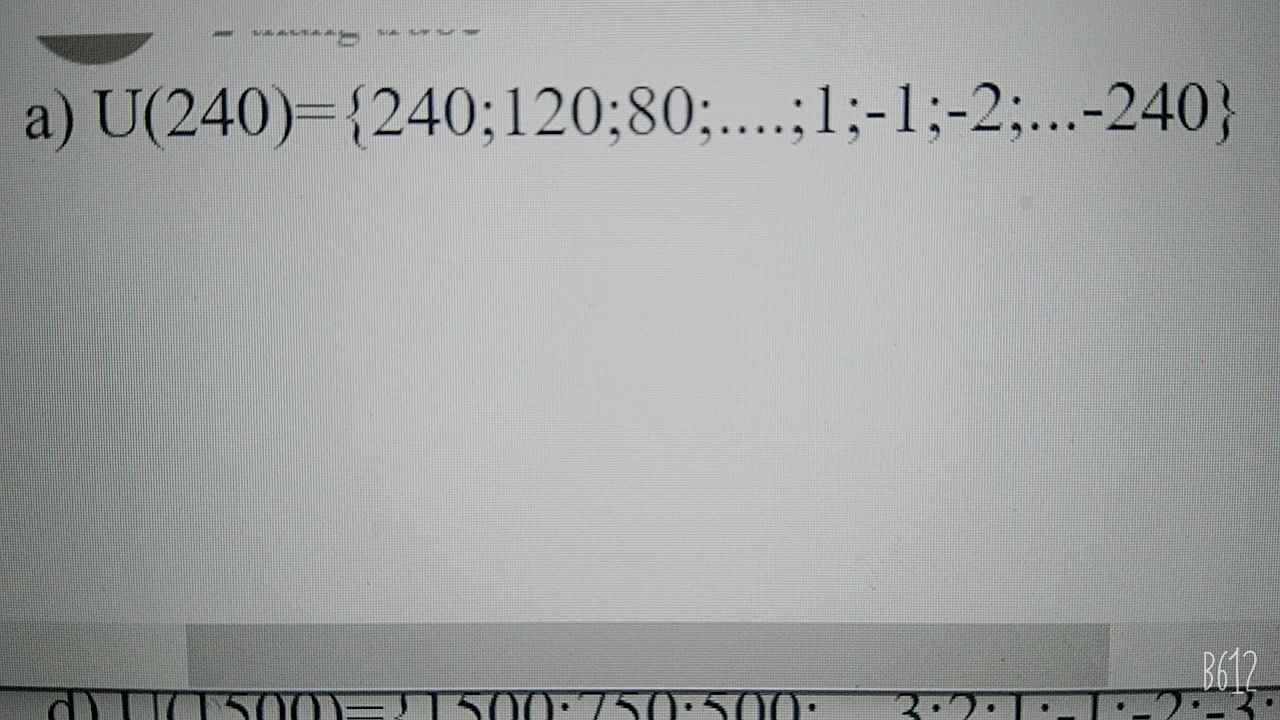
tìm ƯC của 1000 và 128
NT
Những câu hỏi liên quan
hãy tìm ƯCLN(150 và 1000) rồi tìm ƯC(150 và 1000)
\(150=5^2\cdot2\cdot3;1000=2^3\cdot5^3\)
=>\(ƯCLN\left(150;1000\right)=5^2\cdot2=50\)
=>\(ƯC\left(150;1000\right)=Ư\left(50\right)=\left\{1;-1;2;-2;5;-5;10;-10;25;-25;50;-50\right\}\)
Đúng 0
Bình luận (1)
Ta có:
150=2.3.52
1000=23.52.7
=>ƯCLN(150;1000)=2.5=10
=>ƯC(150;1000)={1;2;5;10}
Đúng 0
Bình luận (0)
Ta có:
150=2.3.52
1000=23.52.7
=>ƯCLN(150;1000)=2.5=10
=>ƯC(150;1000)={-1;-2;-5;-10;1;2;5;10}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Ưc của 128 và 240 giúp mik nha
![]()
ta có: 128 = 27
240= 24.3.5
=>ƯCLN(128,240)=24=16
=>ƯC(128,240)=Ư(16)={1;2;4;8;16}
vậy ƯC(128,240)={1;2;4;8;16}
tic cho mình nha
Đúng 1
Bình luận (0)
\(ƯC\left(128,240\right)\)
\(128=2^7\)
\(240=2^4.3.5\)
\(ƯCLN(128,240) =2^4 = 16\)
\(ƯC\left(128;240\right)=ƯC\left(16\right)=\left\{1;2;4;8;16\right\}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
1. Tìm ƯCLN rồi tìm ƯC của:
a. 8; 9
b. 15; 19
c. 8; 32
d. 24; 16; 8
e. 16; 32; 128
f. 105; 128; 135
câu 1 : Số ƯC của hai số 16 và 64 là ...
câu 2 : Số ƯC của số 1339 là ...
câu 3 : Tìm x biết : 17 chia hết cho ( x - 1 ) và ( x - 1 ) chia hết cho 17 . kết quả là ...
câu 4 : Tìm số tự nhiên n , biết rằng : 1+2+3+...+n = 1275 . kết quả n là ...
câu 5 : Tìm BC khác 0 và nhỏ hơn 1000 của 3 số 40 , 60 và 70 . BC đó là ...
1.ƯC (10;20) :
2.100.[10.5.(5^3+3^5)]
3.5.100+10-100
4.Tìm x
a)1000.(x+1000-1^3)=0
b)5000-x:10^3=0
1.Ta có:
Ư(10)={1;2;5;10}.
Ư(20)={1;2;4;5;10;20}.
=> Ư(10;20)={1;2;5;10}
Cái dấu ^ là gì rồi tôi giải tiếp cho
Đúng 0
Bình luận (0)
B1) Tìm ƯC của n + 1 và 3n + 4 với n thuộc tập hợp N.
B2) Tìm ƯC của 30n + 4 và 20n + 3 với n thuộc tập hợp N.
a; Gọi ƯCLN(n + 1; 3n + 4) = d
Ta có: \(\left\{{}\begin{matrix}n+1⋮d\\3n+4⋮d\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}3n+3⋮d\\3n+4⋮d\end{matrix}\right.\) ⇒ 3n + 3 - 3n - 4 ⋮ d
⇒ (3n -3n) - (4 - 3) ⋮ d ⇒ 0 - 1⋮ d ⇒ 1 ⋮ d ⇒ d \(\in\) Ư(1) = 1
Vậy ƯCLN(n + 1; 3n + 4) = 1
ƯC(n +1; 3n +4) = 1
Đúng 0
Bình luận (0)
Gọi ƯCLN(30n + 4; 20n + 3) = d
Ta có: \(\left\{{}\begin{matrix}30n+4⋮d\\20n+3⋮d\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}60n+8⋮d\\60n+6⋮d\end{matrix}\right.\) ⇒ 60n + 8 - 60n - 6 ⋮ d
⇒ (60n - 60n) +(8 - 6) ⋮ d ⇒ 0 +2 ⋮ d ⇒ 2 ⋮ d
⇒ d \(\in\) Ư(2)
Vậy Ước chung lớn nhất của (30n + 4 và 20n + 3) là 2
Đúng 0
Bình luận (0)
5 và 11 tìm ƯCLN và tìm tập hợp của ưc
Tìm ƯCLN rồi tìm ƯC của 36 và 120
\(36=2^2\cdot3^2\\ 120=2^3\cdot3\cdot5\\ ƯCLN\left(36,120\right)=2^2\cdot3=12\\ ƯC\left(36,120\right)=Ư\left(12\right)=\left\{...\right\}\)
Đúng 0
Bình luận (0)
Ta có: 36= 2^2. 3^2
120= 2^3. 3.5
=> ƯCLN( 36; 120)- 2^2. 3= 12
=> ƯC(36;120) = Ư(12) = { 1; 2; 3; 4; 6; 12}
Đúng 0
Bình luận (0)
Ta có: 36 = 22 . 32
120 = 23 . 3 . 5
=> ƯCLN (36, 120) = 22 . 3 = 12
ƯC (36, 120) = ƯCLN (36, 120) = Ư(12) = {1 ; 2 ; 3 ; 4 ; 6 ; 12)
=> ƯC (36, 120) = {1 ; 2 ; 3 ; 4 ; 6 ; 12}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm ƯC và ƯCLN của : 80 và 126
Ư(80)={1;80;2;40;4;20;10;8;5;16}
Ư(126)={1;126;2;63;3;19;14}
Đúng 0
Bình luận (0)
80= 24 .5
120= 23 .3.5
ƯCLN (80,120)= 23.5= 40
ƯC(80,120)= Ư(40)= 1,2,4,5,8,10,20,40
Đúng 0
Bình luận (0)