CMR: f(x) chia hết cho g(x) với
f(x)= x95+x94+x93+…+x2+x+1
g(x)= x31+x30+….+x2+x+1
NH
Những câu hỏi liên quan
Cho g(x) là 1 đa thức với hệ số nguyên. CM: Đa thức f(x)=x2+x.g(x3)f(x)=x2+x.g(x3) không chia hết cho đa thức: x2−x+1
1, Đa thức f(x) khi chia cho x+1 dư 4 khi chia x2+1 dư 2x+3. Tìm đa thức dư khi chia f(x) cho (x+1)(x2+1)
2, Cho P=(a+b)(b+c)(c+a)-abc với a,b,c là các số nguyên. CMR nếu a+b+c chia hết cho 4 thì P chia hết cho 4
2) Ta có đẳng thức sau: \(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
Chứng minh thì bạn chỉ cần bung 2 vế ra là được.
\(\Rightarrow P=\left(a+b+c\right)\left(ab+bc+ca\right)-2abc\)
Do \(a+b+c⋮4\) nên ta chỉ cần chứng minh \(abc⋮2\) là xong. Thật vậy, nếu cả 3 số a, b,c đều không chia hết cho 2 thì \(a+b+c\) lẻ, vô lí vì \(a+b+c⋮4\). Do đó 1 trong 3 số a, b, c phải chia hết cho 2, suy ra \(abc⋮2\).
Do đó \(P⋮4\)
Đúng 3
Bình luận (0)
giúp mik lm câu này vs ạ
f(x) = x4 – 3x2 + x – 1
g(x) = x4 – x3 + x2 + 5
a) f(x)+g(x)
b)f(x)-g(x)
a) f(x)+g(x) = 2x4 -x3 -2x2+x+4
b) f(x)-g(x) =x3-4x2+x-5
Đúng 0
Bình luận (0)
Giải thích các bước giải:
a) f(x)+g(x)=x4x4 – 3x23x2 + x – 1 + x4x4 - x3x3 + x2x2 + 5
=2x42x4 - x3x3 -2x22x2 +x +4
b)f(x)-g(x)=x4x4 – 3x23x2 + x – 1 - x4x4 + x3x3 - x2x2 - 5
= x3x3 - 4x24x2 +x -6
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho f(x) mà với mọi x khác 0 thì: f(1)=1;f(1/x)= 1/x2 .f(x) ;f(x1+ x2)=f(x1)+f(x2) với mọi x1+x2k khác 0 và x1;x2 khác 0.CMR: f(5/7)= 5/7
tìm a b để f(x)=3x4-2x3+(a-1)x2+3x+b chia hết cho g(x)=x2-3x+2
Lời giải:
Ta thấy: $x^2-3x+2=(x-1)(x-2)$. Do đó để $f(x)$ chia hết cho $g(x)$ thì $f(x)\vdots x-1$ và $f(x)\vdots x-2$
Tức là $f(1)=f(2)=0$ (theo định lý Bê-du)
$\Leftrightarrow 3-2+(a-1)+3+b=3.2^4-2.2^3+(a-1).2^2+3.2+b=0$
$\Leftrightarrow a+b=-3$ và $4a+b=-34$
$\Rightarrow a=\frac{-31}{3}$ và $b=\frac{22}{3}$
Đúng 1
Bình luận (0)
1) đa thức f(x)=x^6-x^3+x^2-x+1 có hay ko có nghiệm trên tập hợp số thưc r
2)cho hàm số f(x) xác định với mọi x khác thỏa mãn : f(1)=1 và f(x1 +x2)=f(x1)+f (x2)với mọi x1,x2 jkhacs 0 , x1 + x2 cũng khác 0 và f (1/x)=1/x^2 . f(x) . CMR : f)5/7)=5/7
Cho hàm số y = f(x) xác định với mọi x thuộc Q và có tính chất f(x1) + f(x2) = f(x1+ x2) với mọi x1 x2 thuộc Q . CMR f(-x) = -f (x )
cho f(x)=x^2+p*x+q
g(x)=x^2+p,*x+q,
Chứng minh rằng nếu có hai giá trị x1khacs x2 của x sao cho f(x1)= g(x2);f(x2)=g(x2) thì f(x)=g(x)với mọi x
CMR giá trị của các biểu thức sau không âm với mọi giá trị của biến x: E = x2 + 6x + 11 F = x2 – x + 1 G = x2 + x + 1
\(E=x^2+6x+11\)
\(=x^2+6x+9+2\)
\(=\left(x+3\right)^2+2>0\forall x\)
\(F=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
Đúng 0
Bình luận (1)
Cho đa thức f(x)
x
4
–
3
x
3
+
3
x
2
+ ax + b và đa thức g(x)
x
2
– 3x + 4. Biết f(x) chia hết cho g(x). Khi đó tích a.b bằng A. -12 B. 12 C. -6 D. -8
Đọc tiếp
Cho đa thức f(x) = x 4 – 3 x 3 + 3 x 2 + ax + b và đa thức g(x) = x 2 – 3x + 4. Biết f(x) chia hết cho g(x). Khi đó tích a.b bằng
A. -12
B. 12
C. -6
D. -8
Ta có
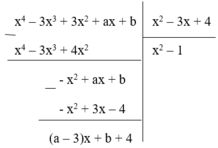
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A
Đúng 1
Bình luận (0)