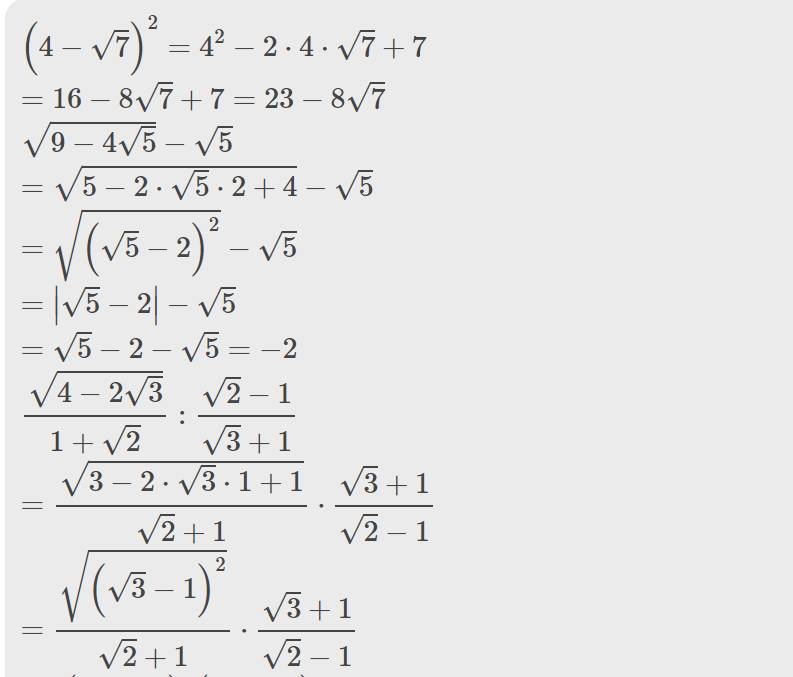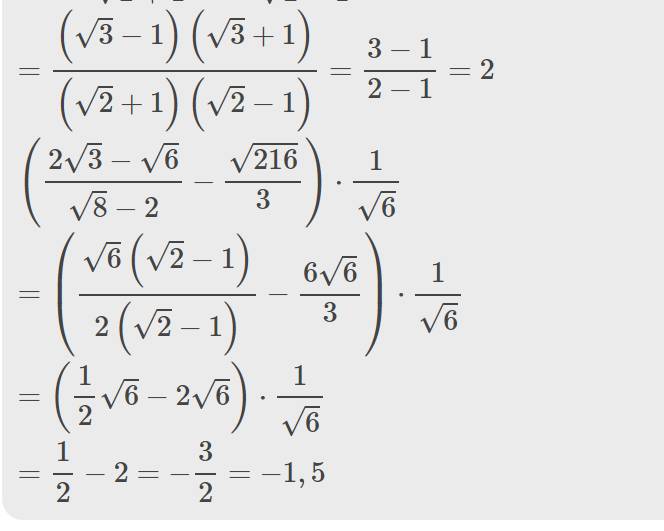\(=\left(2\sqrt{3}-2\sqrt{6}\right)\cdot\sqrt{6}=6\sqrt{2}-12\)

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)

\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)

\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)

\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)

\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)

\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)

\(=\sqrt{5}-2-\sqrt{5}=-2\)

\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)

\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)

\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)

\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)

\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)

\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)

\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)

\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)

\(VT=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)

\(=\left(\dfrac{\sqrt{6}}{2}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)

\(=\dfrac{1}{2}-2=-\dfrac{3}{2}\)

\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}\)

\(=\left(\dfrac{\sqrt{2^2.3}-\sqrt{6}}{2\sqrt{2}-2}-2\sqrt{6}\right).\dfrac{1}{\sqrt{6}}\)

\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2-1}\right)}-2\sqrt{6}\right).\dfrac{1}{\sqrt{6}}\)

\(=\left(\dfrac{\sqrt{6}}{2}-2\sqrt{6}\right).\dfrac{1}{\sqrt{6}}=\sqrt{6}\left(\sqrt{\dfrac{1}{2}}-2\right).\dfrac{1}{\sqrt{6}}=\dfrac{1}{2}-2=\dfrac{-3}{2}=VP\left(đpcm\right)\)

phân tích vế trái trc nha bạn

\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}=\dfrac{-3}{2}\)

\(vt=\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}\)

=\(\left(\dfrac{\sqrt{6}}{2}-\dfrac{6\sqrt{6}}{3}\right).\dfrac{1}{\sqrt{6}}\)

=\(\dfrac{-9\sqrt{6}}{6}.\dfrac{1}{\sqrt{6}}=-\dfrac{3}{2}\)

\(vt=\dfrac{-3}{2}=vp\left(đpcm\right)\)

a)\(\sqrt{\dfrac{2}{2-\sqrt{3}}}=\sqrt{\dfrac{2\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}}\)\(=\sqrt{2\left(2+\sqrt{3}\right)}=\sqrt{4+2\sqrt{3}}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)

b)\(\sqrt{\dfrac{2}{3}}-\sqrt{24}+2\sqrt{\dfrac{3}{8}}+\dfrac{1}{6}=\dfrac{\sqrt{6}}{3}-\sqrt{2^2.6}+\dfrac{2\sqrt{24}}{8}+\dfrac{1}{6}\)

\(=\dfrac{\sqrt{6}}{3}-2\sqrt{6}+\dfrac{\sqrt{2^2.6}}{4}+\dfrac{1}{6}=\dfrac{-5\sqrt{6}}{3}+\dfrac{2\sqrt{6}}{4}+\dfrac{1}{6}\)

\(=\dfrac{-7\sqrt{6}}{6}+\dfrac{1}{6}\)

\(B=\sqrt{9+4\sqrt{5}}+\sqrt{9-4\sqrt{5}}\)

\(B=\sqrt{\left(\sqrt{5}+2\right)^2}+\sqrt{\left(\sqrt{5}-2\right)^2}\)

\(B=\left|\sqrt{5}+2\right|+\left|\sqrt{5}-2\right|\)

\(B=\sqrt{5}+2+\sqrt{5}-2\)

\(B=2\sqrt{5}\)

\(A=\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}\)

\(A=\left(\dfrac{\sqrt{12}-\sqrt{6}}{2\sqrt{2}-2}-\dfrac{6\sqrt{6}}{3}\right).\dfrac{1}{\sqrt{6}}\)

\(A=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-2\sqrt{6}\right).\dfrac{1}{\sqrt{6}}\)

\(A=\left(\sqrt{6}-2\sqrt{6}\right).\dfrac{1}{\sqrt{6}}\)

\(A=-\sqrt{6}.\dfrac{1}{\sqrt{6}}\)

\(A=-1\)

\(\frac{1}{(n+1)\sqrt{n}+n\sqrt{n+1} }=\frac{1}{\sqrt{n(n+1)}(\sqrt{n+1)+\sqrt{n}) } } =\frac{\sqrt{n+1}-\sqrt{n} }{\sqrt{n(n+1)} } =\frac{1}{\sqrt{n} }-\frac{1}{\sqrt{n+1} } \)

=>K=1-\( \frac{1}{5} \)=\(\frac{4}{5} \)

\(\sqrt{15-\sqrt{216}}+\sqrt{33-12\sqrt{6}}=\sqrt{6-6\sqrt{6}+9}+\sqrt{24-12\sqrt{6}+9}=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(\sqrt{24}-3\right)^2}=\left|3-\sqrt{6}\right|+\left|\sqrt{24}-3\right|=3-\sqrt{6}+\sqrt{24}-3=2\sqrt{6}-\sqrt{6}=\sqrt{6}\)

\(\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{30}+\sqrt{162}}=-\dfrac{\sqrt{2}\left(\sqrt{6}-4\right)}{\sqrt{3}\left(\sqrt{6}-4\right)}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{6}\left(\sqrt{5}+\sqrt{27}\right)}=\dfrac{-\sqrt{2}}{\sqrt{3}}-\dfrac{1}{\sqrt{6}}=\dfrac{-\sqrt{6}}{3}-\dfrac{\sqrt{6}}{6}=-\dfrac{\sqrt{6}}{2}\).

\(\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}+\sqrt{\dfrac{2+\sqrt{3}}{2-\sqrt{3}}}=\dfrac{\left(\sqrt{2-\sqrt{3}}\right)^2+\left(\sqrt{2+\sqrt{3}}\right)^2}{\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}}=\dfrac{4}{1}=4\)