tìm số ngyên x,y biết
(x-2)x(y+3)=6
tìm x,y ngyên biết : x.y+ 3.x - y= 6
x.y+3x-y=6
<=> x(y+3)-y-3=6-3
<=>x(y+3)-(y+3)=3
=>(y+3)(x-1)=3=1.3=-1.-3
*) x-1=1;y+3=3=>x=2;y=0
*)x-1=3;y+3=1=>x=4;y=-2
*)x-1=-1;y+3=-3=> x=0;y=0
*)x-1=-3;y+3=-1=>x=-2;y=-2
x.y+3x-y=6
<=> x(y+3)-y-3=6-3
<=>x(y+3)-(y+3)=3
=>(y+3)(x-1)=3=1.3=-1.-3
*) x-1=1;y+3=3=>x=2;y=0
*)x-1=3;y+3=1=>x=4;y=-2
*)x-1=-1;y+3=-3=> x=0;y=0
*)x-1=-3;y+3=-1=>x=-2;y=-2
tìm số ngyên x và y biết: x/7+1/y bằng -1/14 < y khác 0>
x/7+1/y=-1/14
=>\(\dfrac{xy+7}{7y}=\dfrac{-1}{14}\)
=>2xy+14=-y
=>y(2x+1)=-14
=>(2x+1;y) thuộc {(1;-14); (-1;14); (7;-2); (-7;2)}
=>(x,y) thuộc {(0;-14); (-1;14); (3;-2); (-4;2)}
tìm các số ngyên dương x,y biết :
2x-2y=256
ai giúp mik với
Tìm các số ngyên x,y biết:
(2x + 5y + 1)(2|x| + y + x2 +x) =105
Tìm các số ngyên x,y,z biết
-4/8=x/-10=-7/y=z/-24
\(\frac{-4}{8}=\frac{x}{-10}=\frac{-7}{y}=\frac{z}{-24}\)
\(\frac{-4}{8}=\frac{x}{-10}\)=> ( -4 ) . ( -10 ) = 8x => 40 = 8x => x = 5
\(\frac{5}{10}=\frac{-7}{y}\)=> 5y = 10 . ( -7 ) => 5y = -70 => y = -14
\(\frac{-7}{-14}=\frac{z}{-24}\)=> ( -7 ) . ( -24 ) = -14z => 168 = -14z => z = -12
@Quỳnh , dấu sai kìa.
\(\frac{-4}{8}=\frac{x}{-10}=\frac{-7}{y}=\frac{z}{-24}\)
Xét : \(\frac{-4}{8}=\frac{x}{-10}\Leftrightarrow40=8x\Leftrightarrow x=5\)
Xét : \(\frac{-7}{y}=\frac{-4}{8}\Leftrightarrow-56=-4y\Leftrightarrow y=14\)
Xét : \(\frac{-4}{8}=\frac{z}{-24}\Leftrightarrow96=8z\Leftrightarrow z=12\)
tìm số ngyên x,y biết: 3xy - 2x + 5y = 9
Lời giải:
$3xy-2x+5y=9$
$x(3y-2)+5y=9$
$3x(3y-2)+15y=27$
$3x(3y-2)+5(3y-2)=17$
$(3x+5)(3y-2)=17$
Do $x,y$ nguyên nên $3x+5, 3y-2$ cũng là số nguyên. Ta có bảng sau: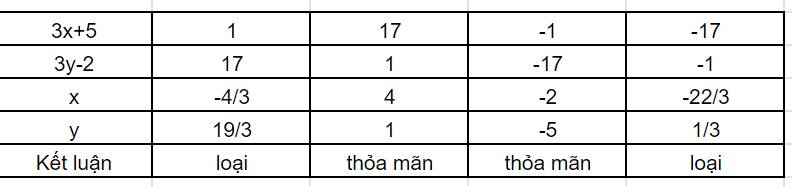
tìm các số ngyên x,y thỏa mãn :
\(x^2-2x=27y^3\)
Tìm 2 số ngyên x, y
(x + 1) mũ 22 . (y - 3) mũ 12 = 0
GIÚP MIK NHA AI NHANH MIK TICK CHO
Từ đề bài, suy ra:
(x+1)22=0 hoặc (y-3)12=0
<=> x+1=0 hoặc y-3=0
<=> x=-1 hoặc y=3
Vậy x\(\in\){-1;3}
woa! thanks Gà Mờ nha
tìm số ngyên x,y thoả mãn
y\(^2\)+2xy-3x-2=0
giúp mik vs ạ
Lời giải:
$y^2+2xy-3x-2=0$
$\Leftrightarrow y^2+2xy+x^2=x^2+3x+2$
$\Leftrightarrow (x+y)^2=(x+1)(x+2)$
Dễ thấy với mọi $x\in\mathbb{Z}$ thì $(x+1, x+2)=1$ nên để tích của chúng là scp thì $x+1, x+2$ cũng là scp
Đặt $x+1=a^2; x+2=b^2$ với $a,b\in\mathbb{Z}$
$\Rightarrow 1=b^2-a^2=(b-a)(b+a)$
$\Rightarrow b-a=b+a=1$ hoặc $b-a=b+a=-1$
$\Rightarrow a=0\Rightarrow x=-1$
Khi đó:
$(x+y)^2=(x+1)(x+2)=0$
$\Rightarrow y=-x=1$
Vậy $(x,y)=(-1,1)$