e cần lời giải chi tiết 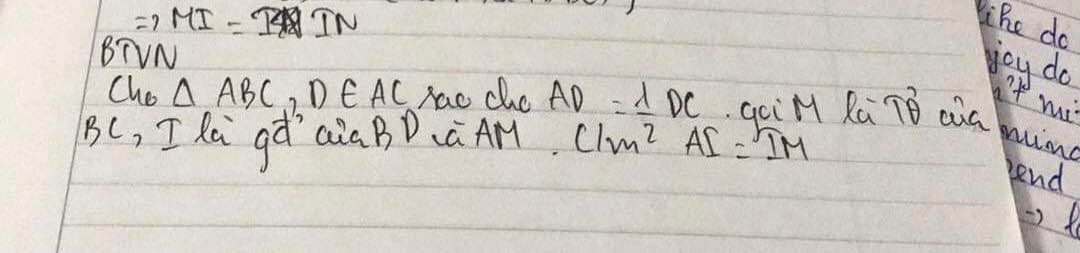
H24
Những câu hỏi liên quan
e cần lời giải chi tiết ạ
đề đâu, mà giải chi tiết thì đăng 1 câu hỏi trong 1 lần đăng thôi
Đúng 0
Bình luận (0)
\(a,x^3+9x^2+27x+27=\left(x+3\right)^3\\ b,\dfrac{x^3}{8}+\dfrac{3}{4}x^2y^2+\dfrac{3}{2}xy^4+y^6=\left(\dfrac{x}{2}+y^2\right)^3\\ c,x^3+6x^2+12x+8=\left(x+2\right)^3\\ d,27x^3-54x^2y+36xy^2-8y^3=\left(3x-2y\right)^3\\ e,8x^6-12x^4+6x^2-1=\left(2x^2-1\right)^3\)
Đúng 1
Bình luận (1)
a: \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b: \(\dfrac{x^3}{8}+\dfrac{3}{4}x^2y^2+\dfrac{3}{2}xy^4+y^6=\left(\dfrac{1}{2}x+y^2\right)^3\)
c: \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
d: \(27x^3-54x^2y+36xy^2-8y^3=\left(3x-2y\right)^3\)
e: \(8x^6-12x^4+6x^2-1=\left(2x^2-1\right)^3\)
Đúng 0
Bình luận (0)
e cần lời giải chi tiết ạ 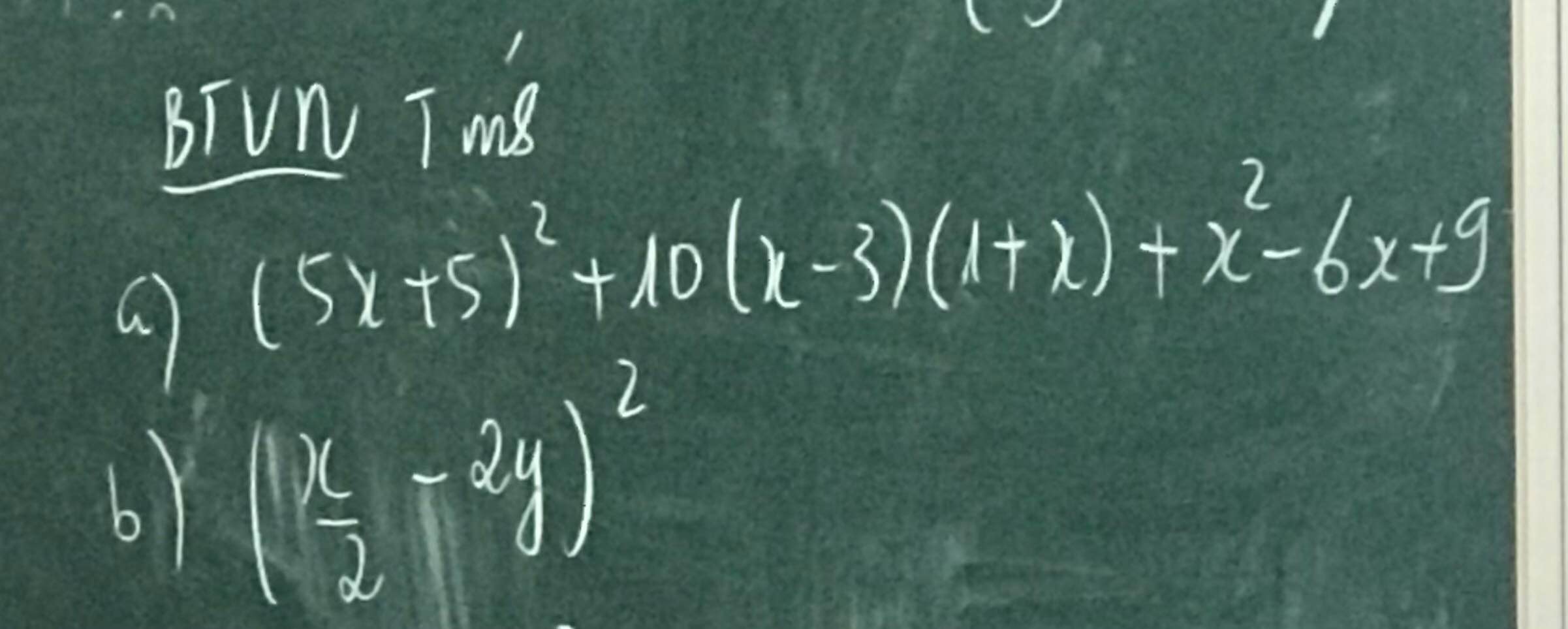
a) \(\left(5x+5\right)^2+10\left(x-3\right)\left(1+x\right)+x^2-6x+9=\left[5\left(x+1\right)\right]^2+2.5\left(x+1\right)\left(x-3\right)+\left(x-3\right)^2=\left[5\left(x+1\right)+\left(x-3\right)\right]^2=\left(5x+5+x-3\right)^2=\left(6x+2\right)^2=\left(6x\right)^2+2.6x.2+2^2=36x^2+24x+4\)
b) \(\left(\dfrac{x}{2}-2y\right)^2=\left(\dfrac{x}{2}\right)^2-2.\dfrac{x}{2}.2y+\left(2y\right)^2=\dfrac{x^2}{4}-2xy+4y^2\)
Đúng 1
Bình luận (0)
a: \(\left(5x+5\right)^2+10\left(x-3\right)\left(x+1\right)+x^2-6x+9\)
\(=\left[5\left(x+1\right)\right]^2+2\cdot5\left(x+1\right)\cdot\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(5x+5+x-3\right)^2\)
\(=\left(6x+2\right)^2\)
b: \(\left(\dfrac{1}{2}x-2y\right)^2=\dfrac{1}{4}x^2-2xy+4y^2\)
Đúng 0
Bình luận (0)
giúp e giải gấp với ạ e cần lời giải chi tiết ạ e cảm ơn


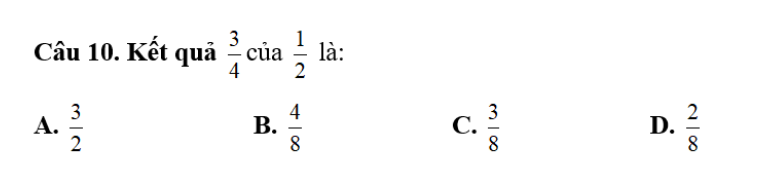
e cần xem cần lời giải chi tiết kèm đáp án ạ
Xem thêm câu trả lời
Bài 5: Tìm số E=\(\overline{xyzt}\) biết E - 2. \(\overline{yzt}\)=\(\overline{xz}\).
Mình cần gấp ạ mong các bạn giúp mình.Mình cần lời giải chi tiết ạ
\(E-2\overline{yzt}=\overline{xz}\)
=>1000x+100y+10z+t-200y-20z-20t=10x+z
=>990x-100y-11z-19t=0
=>\(\left(x,y,z,t\right)\in\varnothing\)
Đúng 0
Bình luận (0)
tìm GTLN của biểu thức:
\(E=\dfrac{5x^2+15}{2x^2+3}\)
giúp mk với ạ cần lời giải chi tiết nhé![]()
\(E=\dfrac{\dfrac{5}{2}\left(2x^2+3\right)+\dfrac{15}{2}}{2x^2+3}=\dfrac{5}{2}+\dfrac{15}{2\left(2x^2+3\right)}\)
Do \(2x^2+3\ge3;\forall x\Rightarrow\dfrac{15}{2\left(2x^2+3\right)}\le\dfrac{15}{2.3}=\dfrac{5}{2}\)
\(\Rightarrow E\le\dfrac{5}{2}+\dfrac{5}{2}=5\)
\(E_{max}=5\) khi \(x=0\)
Đúng 1
Bình luận (0)
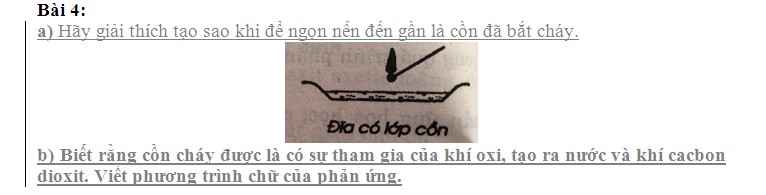 mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn
mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn
Chứng minh rằng : x^2-2xy+y^2+1 >0 với mọi số thực x,y Giúo e với ạ. Em cần lời giải chi tiết
Ta có: \(x^2-2xy+y^2+1=\left(x-y\right)^2+1\)
Vì \(\left(x-y\right)^2\ge0\forall x,y\)
Mà \(1>0\)
\(\Rightarrow\left(x-y\right)^2+1>0\forall x,y\left(đpcm\right)\)
Đúng 1
Bình luận (0)
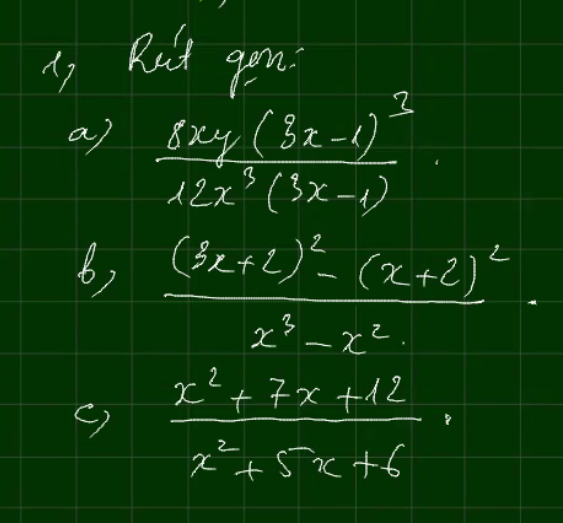
cần lời giải chi tiết
\(a,=\dfrac{2y\left(3x-1\right)^2}{3x^2}\\ b,=\dfrac{\left(3x+2-x-2\right)\left(3x+2+x+2\right)}{x^2\left(x-1\right)}\\ =\dfrac{2x\left(4x+4\right)}{x^2\left(x-1\right)}=\dfrac{8\left(x+1\right)}{x\left(x-1\right)}\\ c,=\dfrac{x^2+3x+4x+12}{x^2+2x+3x+6}\\ =\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x+2\right)\left(x+3\right)}=\dfrac{x+4}{x+2}\)
Đúng 4
Bình luận (1)









