4tan ruoi +50kg =
MH
Những câu hỏi liên quan
tong cua 4 tan ruoi + voi 50kg=...kg
4 tấn rưỡi + 50kg = 4500 + 50 = 4550kg
Đúng 0
Bình luận (0)
tổng 4 tan ruoi + 50kg =...kg
mot thua ruong hinh chu nhatco chu vi la 300m.biet chieu dai gap ruoi chieu rong. hoi
a) tinh dien tich thua ruong do.
b)biet rang cu 100m vuong thu hoach duoc 50kg thoc.oi tren ca thua ruong do nguoi ta thu hoach duoc bao nhieu ta thoc
a la 5000mvuong
thu duoc 2500kgthoc=15ta thoc
Đúng 0
Bình luận (0)
4tan 18dg=...tan
1/4tan = ..........kg
250 kg nha bạn! Chúc bạn học tốt !
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Nếu
tan
β
2
4
tan
α
2
thì
tan
β
-
α
2
bằng :
Đọc tiếp
Nếu tan β 2 = 4 tan α 2 thì tan β - α 2 bằng :
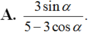
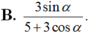
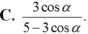
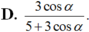
Chọn A.
Sử dụng công thức cộng ; ta có:
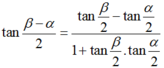
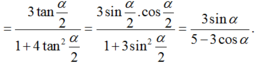
Đúng 0
Bình luận (0)
2.Viết các số đo sau dưới dạng số đo có đơn vị là mét vuông.
6,7dm2 0,234dm2 0,072dm2 406.005dm2
3.Viet so thích hợp vào chỗ chấm.
23m2 7cm2=.............cm2 4tan 34kg=................kg
23m2 7cm2=..................m2 4tan 34kg=...................tan
câu 2 : 0.067m2; 0.00234m2,0.00072m2;4.06005m2
câu 3 : 230007cm2;23.0007m2;4034kg;4.034tan
Đúng 0
Bình luận (0)
Cho hàm số f(x) = cos19x và g(x) = 4tan 3x, chọn mệnh đề đúng
A. f(x) là hàm số chẵn, g(x) là hàm số lẻ.
B. f(x) là hàm số lẻ, g(x) là hàm số chẵn.
C. f(x) và g(x) đều là hàm số chẵn.
D. f(x) và g(x) đều là hàm số lẻ.
+ Xét hàm y= f(x)= cos 19x
TXĐ: D= R
Với mọi x ∈ ℝ , ta có: - x ∈ ℝ và
f(- x) = cos( -19x)= cos19x = f(x)
Do đó y= cos19x là hàm số chẵn trên R.
+ Xét hàm y= g(x) = 4tan3x
TXĐ: D = ℝ \ { π 6 + k π 3 , k ∈ ℤ }
Với mọi x ∈ ℝ , ta có: - x ∈ ℝ và
g(-x) = 4.tan(- 3x) = - 4tan 3x= - g(x)
Do đó: y= 4tan3x là hàm lẻ trên tập xác định của nó
Đáp án A
Đúng 0
Bình luận (0)
giải pt
tan4x - 4tan2x + 3=0
ĐKXĐ: ...
\(\Leftrightarrow\left(tan^2x-1\right)\left(tan^2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tan^2x=1\\tan^2x=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}sin^2x=cos^2x\\sin^2x=3cos^2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^2x-sin^2x=0\\\frac{1}{2}-\frac{1}{2}cos2x=\frac{3}{2}+\frac{3}{2}cos2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\pm\frac{\pi}{3}+k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)

