: Cho hình bình hành ABCD có tâm O. Tìm các vecto sau
a) BD-BA
b)bc-bd+ba
c)oc+ab-do
d)ad-ba-ao
Cho hình bình hành ABCD tâm O chứng minh các vecto BD-BA=OC-OB Giúp mình với ạ
\(\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BO}+\overrightarrow{OC}=\overrightarrow{BC}\)(1)
ABCD là hình bình hành
=>\(\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}\)
=>\(\overrightarrow{BC}=\overrightarrow{BD}-\overrightarrow{BA}\left(2\right)\)
Từ (1) và (2) suy ra \(\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BD}-\overrightarrow{BA}\)
Câu 1: giả sử:\(\overrightarrow{BD}-\overrightarrow{BA}=\overrightarrow{OC}-\overrightarrow{OB}\Leftrightarrow\overrightarrow{BA}+\overrightarrow{AD}-\overrightarrow{BA}=\overrightarrow{OC}+\overrightarrow{BO}\)
\(\Leftrightarrow\overrightarrow{AD}=\overrightarrow{BC}\)(luôn đúng vì ABCD lad hình bình hành)
giả sử: \(\overrightarrow{BC}-\overrightarrow{BD}+\overrightarrow{BA}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BC}-\overrightarrow{BC}+\overrightarrow{DC}+\overrightarrow{BA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BB}+\overrightarrow{DD}=\overrightarrow{0}\)(LUÔN ĐÚNG)
câu 2 :GIẢ SỬ:
\(\overrightarrow{AB}+\overrightarrow{OA}=\overrightarrow{OB}\Leftrightarrow\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{0}\)(luôn đúng)
giả sử: \(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}\\ \Leftrightarrow\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}=\overrightarrow{MB}+\overrightarrow{MD}\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\)
Cho hình bình hành ABCD có tâm O. CMR
a/ vecto AB+OD+OC=AC
b/ vecto BA+BC+OB=OD
c/ vecto BA+BC=MO-MB-OB
Cho hình bình hành ABCD có AB = 4, AD = 6, \(\widehat {BAD} = {60^o}\) (Hình 73).
a) Biểu thị các vecto \(\overrightarrow {BD} ,\overrightarrow {AC} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} .\)
b) Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AD} ,\;\overrightarrow {AB} .\overrightarrow {AC} ,\;\overrightarrow {BD} .\overrightarrow {AC} .\)
c) Tính độ dài các đường chéo \(BD,AC.\)
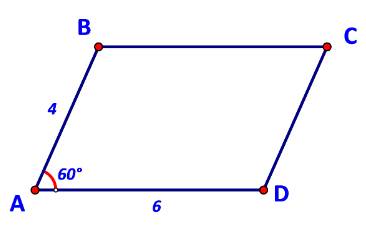
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)
Cho hình bình hành ABCD tâm O. Gọi trung điểm của BC, CD theo thứ tự là P, Q. Hãy biểu diễn các vecto BC, AP, AQ, PQ theo các vecto AB và AO
có ai biết làm toán hình ko chỉ mình với
BÀI 1 : Cho hình bình hành ABCD tâm O . chứng minh rằng :
a) vecto CO - vecto OB = vecto BA b) vecto AB - vecto BC = vecto DB
c) vecto DA - vecto DB = vecto OD - vecto OC d) vecto DA - vecto DB + vecto DC = vecto O
BÀI 2 : chứng minh rằng 4 điểm A,B,C,D bất kì ta có :
vecto AC + vecto BD = vecto AD + vecto BC
BÀI 3 : cho tứ giác ABCD . Gọi I , J là trung điểm AD , BC ; P là trung điểm IJ.
a) tính vecto AB + vecto DC + vecto BD + vecto CA
b) CMR : vecto AB + vecto CD = vecto AD + vecto CB , vecto AB + vecto DC = 2IJ
c) CMR : vecto PA + vecto PB + vecto PC + vecto PD = vecto 0 , vecto AB + vecto AC + vecto AD = 4AP
MÌNH CẦN GẤP LẮM GIÚP MÌNH NHA
bài 1
a CO-OB=BA
<=.> CO = BA +OB
<=> CO=OA ( LUÔN ĐÚNG )=>ĐPCM
b AB-BC=DB
<=> AB=DB+BC
<=> AB=DC(LUÔN ĐÚNG )=> ĐPCM
Cc DA-DB=OD-OC
<=> DA+BD= OD+CO
<=> BA= CD (LUÔN ĐÚNG )=> ĐPCM
d DA-DB+DC=0
VT= DA +BD+DC
= BA+DC
Mà BA=CD(CMT)
=> VT= CD+DC=O
BÀI 2
AC=AB+BC
BD=BA+AD
=> AC+BD= AB+BC+BA+AD=BC+AD (đpcm)
Trên hình bình hành abcd tâm o lấy m n sao cho vecto am=vecto mb vectoan=2vectond.gọi k h lần lượt là trung điểm mn oc biểu diễn kh theo vecto ad ab
\(\overrightarrow{AM}=\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AB}=-\overrightarrow{AM}+\overrightarrow{AB}\Rightarrow2\overrightarrow{AM}=\overrightarrow{AB}\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{AN}=2\overrightarrow{ND}=2\left(\overrightarrow{NA}+\overrightarrow{AD}\right)=-2\overrightarrow{AN}+2\overrightarrow{AD}\Rightarrow3\overrightarrow{AN}=2\overrightarrow{AD}\Rightarrow\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AD}\)
Do K là trung điểm MN
\(\Rightarrow\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
Theo tính chất hbh: \(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
Do O là tâm hình bình hành \(\Rightarrow\overrightarrow{AO}=\overrightarrow{OC}=\dfrac{1}{2}\overrightarrow{AC}\)
Mà H là trung điểm OC \(\Rightarrow\overrightarrow{OH}=\dfrac{1}{2}\overrightarrow{OC}=\dfrac{1}{4}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AH}=\overrightarrow{AO}+\overrightarrow{OH}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{KH}=\overrightarrow{KA}+\overrightarrow{AH}=-\overrightarrow{AK}+\overrightarrow{AH}\)
\(=-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{5}{12}\overrightarrow{AD}\)
\(\overrightarrow{AN}=2\overrightarrow{ND}\)
=>A,N,D thẳng hàng và AN=2ND
ABCD là hình bình hành tâm O
=>O là trung điểm chung của AC và BD
H là trung điểm của OC
nên HO=HC=1/2CO
=>\(HO=HC=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot CA=\dfrac{1}{4}CA\)
\(\overrightarrow{AM}=\overrightarrow{MB}\)
=>AM=MB và M nằm giữa A và B
=>M là trung điểm của AB
AN+ND=AD
=>2ND+ND=AD
=>AD=3ND
=>AN/AD=2/3
=>\(\overrightarrow{AN}=\dfrac{2}{3}\cdot\overrightarrow{AD}\)
\(\overrightarrow{KH}=\overrightarrow{KM}+\overrightarrow{MH}\)
\(=\dfrac{1}{2}\overrightarrow{NM}+\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CH}\)
\(=\dfrac{1}{2}\left(\overrightarrow{NA}+\overrightarrow{AM}\right)+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}+\dfrac{1}{4}\overrightarrow{CA}\)
\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right)+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{4}\left(\overrightarrow{CD}+\overrightarrow{CB}\right)\)
\(=-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{5}{12}\overrightarrow{AD}\)
31/ Cho hình bình hành ABCD có AC cắt BD tại O. Đáp án nào sau đây đúng:
A. OA = OB; OC = OD. B. OA = OD; OB = OC
C. OA = OC; OB = OD. D. AB = BC; CD = AD
Cho hình bình hành ABCD. Trên các cạnh AB; BC; CD; DA lấy các điểm E; F; G; H sao cho AE = CG; BF = DH. CMR:
a, Xác định tâm đối xứng của hình bình hành ABCD
b, EFGH là hình bình hành và tìm tâm đối xứng
c, Gọi O là giao điểm của AC và BD, O còn là tâm đối xứng của hình bình hành nào?