Giúp mình câu f với ạ
MO
Những câu hỏi liên quan
 Giúp mình câu f,g,f,k với ạ
Giúp mình câu f,g,f,k với ạ
f: Thay x=0 và y=5 vào (d), ta được:
m-1=5
hay m=6
e: Thay x=1 và y=4 vào (d),ta được:
2m+3+m-1=4
=>3m+2=4
hay m=2/3
Đúng 0
Bình luận (0)

Giúp mình câu f với ạ, mình cảm ơn
a: \(A=\dfrac{x}{x-4}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Đúng 0
Bình luận (1)
b: Thay x=36 vào biểu thức \(\dfrac{\sqrt{x}}{\sqrt{x}-2}\), ta có
\(\Rightarrow\dfrac{\sqrt{36}}{\sqrt{36}-2}\Rightarrow\dfrac{6}{6-2}\Rightarrow\dfrac{6}{4}\Rightarrow\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Tiếp của anh Nguyễn Lê Phước Thịnh:
b. Thay x = 36 vào A, ta được:
A = \(\dfrac{\sqrt{36}}{\sqrt{36}-2}=\dfrac{6}{6-2}=\dfrac{6}{4}=\dfrac{3}{2}\)
c. Ta có:
\(\dfrac{\sqrt{x}}{\sqrt{x}-2}=-\dfrac{1}{3}\left(ĐK:x\ge0;x\ne2\right)\)
<=> \(-3\sqrt{x}=\sqrt{x}-2\)
<=> \(2=4\sqrt{x}\)
<=> \(\sqrt{x}=\dfrac{1}{2}\)
<=> \(x=\dfrac{1}{4}\left(TM\right)\)
e. Ta có:
\(\dfrac{\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=-2\)
<=> \(\dfrac{\sqrt{x}}{\sqrt{x}-2}.\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=-2\)
<=> \(\dfrac{\sqrt{x}}{\sqrt{x}+1}=-2\)
<=> \(\sqrt{x}=-2\left(\sqrt{x}+1\right)\)
<=> \(\sqrt{x}=-2\sqrt{x}-2\)
<=> \(\sqrt{x}+2\sqrt{x}=-2\)
<=> \(3\sqrt{x}=-2\)
<=> \(\sqrt{x}=\dfrac{-2}{3}\)
<=> \(x=\dfrac{4}{9}\left(TM\right)\)
Đúng 0
Bình luận (0)
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giải giúp mình từ câu f đến hết ạ mình cảm ơn hứa rate 5 sao ạ
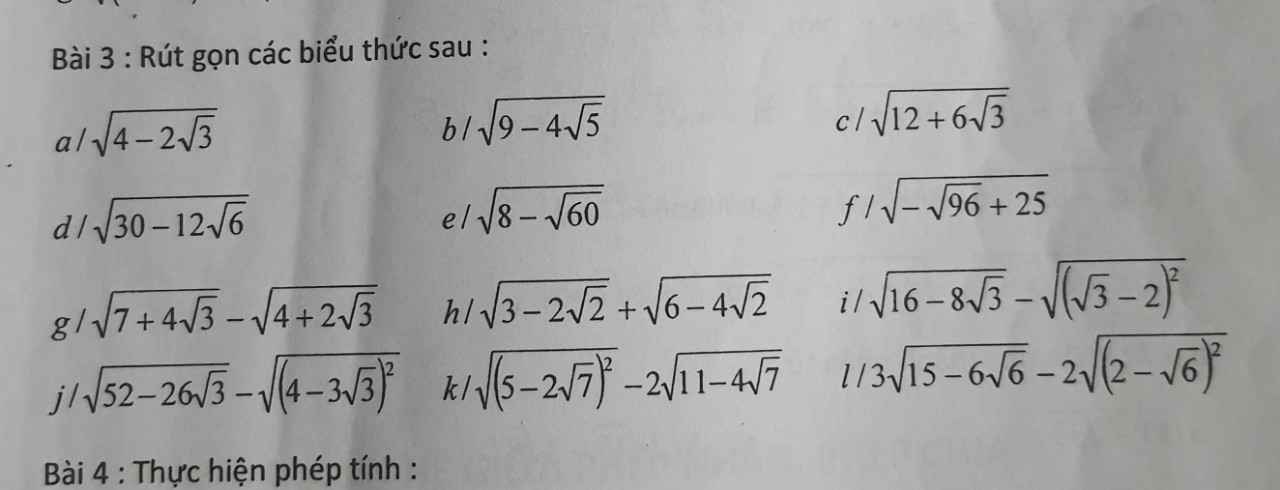
a) \(\sqrt{4-2\sqrt{3}}=\sqrt{3}-1\)
b) \(\sqrt{9-4\sqrt{5}}=\sqrt{10}-1\)
c) \(\sqrt{12+6\sqrt{3}}=3+\sqrt{3}\)
d) \(\sqrt{30-12\sqrt{6}}=3\sqrt{2}-2\sqrt{3}\)
e) \(\sqrt{8-\sqrt{60}}=\sqrt{5}-\sqrt{3}\)
f) \(\sqrt{-\sqrt{96}+25}=2\sqrt{6}-1\)
Đúng 1
Bình luận (1)
g: Ta có: \(\sqrt{7+4\sqrt{3}}-\sqrt{4+2\sqrt{3}}\)
\(=2+\sqrt{3}-\sqrt{3}-1\)
=1
h: Ta có: \(\sqrt{3-2\sqrt{2}}+\sqrt{6-4\sqrt{2}}\)
\(=\sqrt{2}-1+2-\sqrt{2}\)
=1
Đúng 0
Bình luận (0)
giúp mình câu d, e,f, h đi ạ, mình cảm ơn
\(e,=\dfrac{\left(3+\sqrt{2}\right)\left(2\sqrt{2}+1\right)}{7}-\sqrt{\dfrac{\left(\sqrt{2}+1\right)^2}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}}\\ =\dfrac{7\sqrt{2}+7}{7}-\dfrac{\sqrt{2}+1}{1}=\sqrt{2}+1-\sqrt{2}-1=0\)
\(f,=\sqrt{\dfrac{\left(2\sqrt{3}-3\right)^2}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}}\left(2+\sqrt{3}\right)\\ =\dfrac{\left(2\sqrt{3}-3\right)\left(2+\sqrt{3}\right)}{\sqrt{3}}\\ =\dfrac{\sqrt{3}}{\sqrt{3}}=1\)
\(h,=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{20-9}}\left(\sqrt{2}+\sqrt{10}\right)\\ =\sqrt{\dfrac{2\left(33-11\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{\dfrac{22\left(3-\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{6-2\sqrt{5}}\left(\sqrt{5}+1\right)=\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)=4\)
Đúng 4
Bình luận (0)
giúp mình câu a b c e f nhé .Cảm ơn ạ!
b: =>(x+1)(x-1)-(x+3)(x-3)=2x^2+6x
=>2x^2+6x=x^2-1-x^2+9=8
=>2x^2+6x-8=0
=>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1(loại)
a: =>x^3+2x-2x(x^2+1)=0
=>x^3+2x-2x^3-2x=0
=>-x^3=0
=>x=0(nhận)
c: =>(x-2)(x+2)-(x+5)^2=x^2-8
=>x^2-4-x^2-10x-25=x^2-8
=>x^2-8=-10x-29
=>x^2+10x+21=0
=>(x+3)(x+7)=0
=>x=-3 hoặc x=-7
Đúng 0
Bình luận (0)
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
Các bạn giúp mik câu T F NG vs ạ
Mình xin cảm ơn !
Mọi người giúp mình câu này với ạ. Mình cảm ơn nhiều
Một tấm bê tông có trọng lượng 120.000N được kéo chuyển động thẳng đều bởi một lực F. Biết hệ
số ma sát giữa tấm be tông và sàn là 0,45. Tìm F nếu
a. TH 1: Lực F nằm ngang
b. TH2: Lực F có hướng hợp với phương ngang 1 góc 300
Lực F nằm ngang.
\(P=N=120000N\)
Lực ma sát: \(F_{ms}=\mu mg=\mu\cdot N=0,45\cdot120000=54000N\)
Lực kéo F theo phương ngang:
\(F_k=P+F_{ms}=120000+54000=174000N\)
Đúng 2
Bình luận (1)