Cho tam giác nhọn ABC. Trên tia đối của các tia AB, AC lấy lần lượt các điểm D, E sao cho AD=AB; AE=AC. Gọi M, N lần lượt là trung điểm của các đoạn thẳng BC và DE. Chứng minh:
a) \(\Delta ABC=\Delta ADE\)
b) BC // DE
c) AM=AN
d) M, A, N thẳng hàng
HT
Những câu hỏi liên quan
cho tam giác ABC có ba góc nhọn , AB<AC . Vẽ tia đối của tia AB , trên đó lấy điểm D sao cho AD=AC . Vẽ tia đối của tia AC, trên đó lấy điểm E sao cho AE=AB . Lấy hai điểm M,N lần lượt là trung điểm của CD,BE .Chứng minh :
a) tam giác ADM = tam giác ACM
b) tam giác AEN = tam giác ABN
a: Xét ΔADM và ΔACM co
AD=AC
DM=CM
AM chung
=>ΔADM=ΔACM
b: Xét ΔAEN và ΔABN có
AE=AB
EN=BN
AN chung
=>ΔAEN=ΔABN
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (BC AC AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI BI. Vẽ các điểm H, K lần lượt là hình chiếu của I trên AB và ADCho tam giác nhọn ABC (BC AC AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI BI. Vẽ các điểm H,K lần lợt là hình chiếu của I trên AB và AD.a) Chứng minh tam giác ABC là tam giác cân.b) Chứng minh IH IK.c) So sánh IH và ID.Giúp mình với ạ
Đọc tiếp
Cho tam giác nhọn ABC (BC > AC > AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI = BI. Vẽ các điểm H, K lần lượt là hình chiếu của I trên AB và AD
Cho tam giác nhọn ABC (BC > AC > AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI = BI. Vẽ các điểm H,K lần lợt là hình chiếu của I trên AB và AD.
a) Chứng minh tam giác ABC là tam giác cân.
b) Chứng minh IH = IK.
c) So sánh IH và ID.
Giúp mình với ạ
a: Xét ΔABD có
AI vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
góc HAI=góc KAI
=>ΔAHI=ΔAKI
=>HI=KI
c: HI=KI
KI<ID
=>HI<ID
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC (BC AC AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI BI. Vẽ các điểm H, K lần lượt là hình chiếu của I trên AB và ADCho tam giác nhọn ABC (BC AC AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI BI. Vẽ các điểm H,K lần lợt là hình chiếu của I trên AB và AD.a) Chứng minh tam giác ABC là tam giác cân.b) Chứng minh IH IK.c) So sánh IH và ID.Giúp mình với ạ
Đọc tiếp
Cho tam giác nhọn ABC (BC > AC > AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI = BI. Vẽ các điểm H, K lần lượt là hình chiếu của I trên AB và AD
Cho tam giác nhọn ABC (BC > AC > AB), đường cao AI. Trên tia đối của tia IB lấy điểm D sao cho DI = BI. Vẽ các điểm H,K lần lợt là hình chiếu của I trên AB và AD.
a) Chứng minh tam giác ABC là tam giác cân.
b) Chứng minh IH = IK.
c) So sánh IH và ID.
Giúp mình với ạ
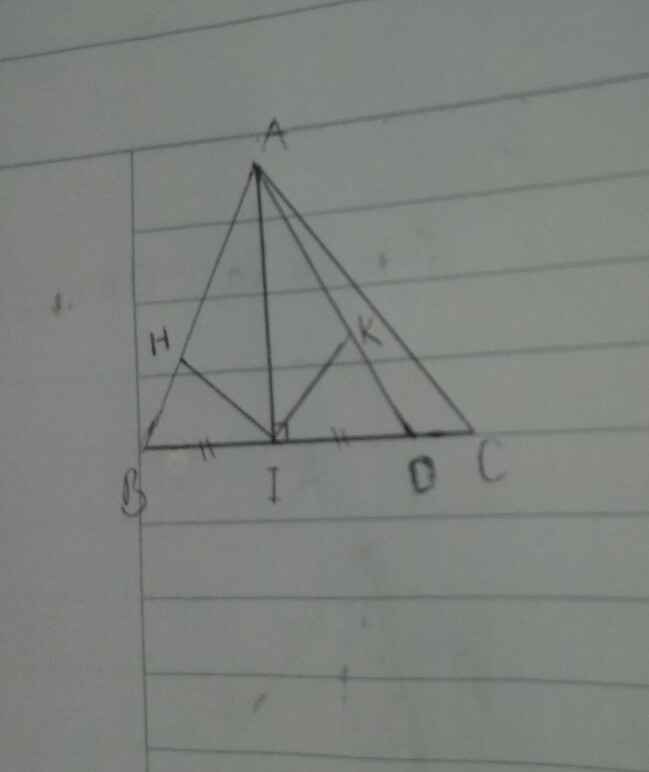
rồi từ câu a) là sai đề nhaaaa em ( ko thể chứng minh đc - do AB < AC < BC)
Đúng 1
Bình luận (1)
Cho tam giác ABC nhọn . Trên tia đối của tia AB lấy điểm D sao cho AD=AB. Trên tia đối của AC lấy điểm E sao cho AE=AC.
1) So sánh BC và DE.
2) AH và AK lần lượt là đường cao của tam giác ABC và ADE. Chứng minh H, A, K thẳng hàng
1: Xét tứ giác BCDE có
A là trung điểm của BD
A là trung điểm của CE
Do đó; BCDE là hình bình hành
Suy ra: BC//DE
2: AH\(\perp\)BC
mà BC//DE
nên \(AH\perp\)DE
mà AK\(\perp\)DE
và AH,AK có điểm chung là A
nên H,A,K thẳng hàng
Đúng 3
Bình luận (1)
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD sao AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC. Gọi M,N lần lượt là các điểm trên tia BC và ED sao cho CM = EN.
CMR: M, A,N thẳng hàng
tg ADE=ABC( AB=AD;AC=AE;A đối đỉnh)
=>gocE=C
xet tg AEN va tgACM bằng nhau( CM=EN;AE=AC;E=C)
=> goc NAE=CAM ( 2 goc nay o vi tri đối đỉnh nên M;A;N
Đúng 2
Bình luận (1)
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD sao AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC. Gọi M,N lần lượt là các điểm trên tia BC và ED sao cho CM = EN. CMR: M, A,N thẳng hàng
cho tam giác abc, AB=4,8cm; BC=3,6cm; AC= 6,4cm. trên AC lấy điểm E sao cho AE=2,4cm; trên AB lấy điểm D sao cho AD= 3,2 cm. gọi giao điểm của BC với ED là F. tính DF
Đúng 1
Bình luận (0)
Có: tam giác ABC đồng dạng với tam giác ADE
=>AB/AD=AC/AE
Có AB/AD=AB/2AB=1/2
AC/AE=AC/2AC=1/2
Vậy tam giác ABC đồng dạng với tam giác ADE the tỉ số đồng dạng là 1/2
Đúng 0
Bình luận (0)
cho tam giác abc nhọn có ab < ac. vẽ tia đối của tia ab, trên đó lấy điểm d sao cho ad= ac. vẽ tia đối của tia ac, trên đó lấy điểm e sao cho ae= ab chứng minh tam giác abc bằng tam giác aed
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy E sao cho AE = AC. Đường thẳng qua A cắt các cạnh DE và BC lần lượt ở M và N. Chứng minh rằng: AM = AN.
cho tam giác ABC. trên tia đối của tia AB lấy điểm D sao cho AB=AD, trên tia đối của tia AC lấy điểm E sao cho AC=AE. một đường đi qua A cắt các cạnh BC và DE lần lượt tại M và N. chúng minh góc ADE=góc ABC; góc AED= góc ACB
Xét tứ giác EDCB có
A là trung điểm của đường chéo DB
A là trung điểm của đường chéo EC
Do đó: EDCB là hình bình hành
Suy ra: ED//BC
hay \(\widehat{ADE}=\widehat{ABC};\widehat{AED}=\widehat{ACB}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC. Trên tia đối của các tia AB, AC lần lượt lấy các điểm D và E sao cho AD= AB và AE= AC
a) Chứng minh: tam giác ABC= tam giác ADE
b) Chứng minh DE // BC
c) Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh A là trung điểm của MN