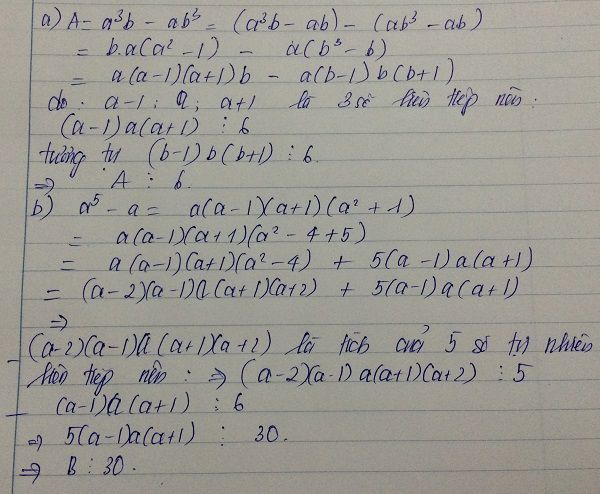Chứng minh rằng với mọi số nguyên a thì \(a^5+29a\) chia hết cho 30
HC
Những câu hỏi liên quan
Chứng minh rằng với mọi số nguyên a thì \(a^5+29a\) chia hết cho 30
\(a^5+29a=a^5-a+30a\)
Theo Fermat nhỏ thì \(a^5-a⋮5\) mặt khác \(a^5-a=a\left(a-1\right)\left(a+1\right)\left(a^2+1\right)⋮6\)
nên \(a^5+29a⋮30\) ( điều phải chứng minh )
Chứng minh rằng với mọi số nguyên a,b, c thì (a−b)^5+(b-c)^5+(c-a)^5
chia hết cho 30.
Link câu trả lời của mk
https://olm.vn/hoi-dap/detail/1309800733128.html
Chứng minh rằng với mọi số nguyên a thì \(a^3-a\) chia hết cho 6, \(a^5-a\) chia hết cho 30
ta có :
\(a^3-a=a\left(a^2-1\right)=a\left(a-1\right)\left(a+1\right)\) là tích của ba số nguyên liên tiếp nên \(a^3-a\text{ chia hết cho 6}\)
ta có : \(a^5-a=a\left(a^4-1\right)=a\left(a-1\right)\left(a+1\right)\left(a^2+1\right)\)
ta có tích trên chia hết cho 6 do chứng minh ở ý trên, ta cần chỉ ra nó chia hết cho 5 nữa.
thật vậy: nếu a=5q hoặc a=5q+1 hoặc a=5q+4 thì a(a-1)(a+1) chia hết cho 5
nếu a=5q+2 hoặc a=5q+3 thì \(a^2+1\text{ chia hết cho 5}\)
vậy \(a^5-a\text{ chia hết cho 30}\)
Ta có a3 - a = a(a2 - 1) = (a - 1)a(a + 1) \(⋮6\)(tích 3 số nguyên liên tiếp)
Ta có a5 - a = a(a4 - 1) = a(a2 - 1)(a2 + 1) = (a - 1)a(a + 1)(a2 + 1)
= (a - 1)a(a + 1)(a2 - 4 + 5)
= (a - 1)a(a + 1)(a2 - 4) + 5(a - 1)a(a + 1)
= (a - 2)(a - 1)a(a + 1)(a + 2) + 5(a - 1)a(a + 1)
Nhận thấy (a - 1)a(a + 1) \(⋮\)6
=> 5(a - 1)a(a + 1) \(⋮\)30
Lại có (a - 2)(a - 1)a(a + 1)(a + 2) \(⋮30\)(tích 5 số nguyên liên tiếp)
=> a - 2)(a - 1)a(a + 1)(a + 2) + 5(a - 1)a(a + 1) \(⋮\)30
=> a5 - a \(⋮30\)
Chứng minh rằng với mọi số nguyên a,b, c thì \(\left(a-b\right)^5+\left(b-c\right)^5+\left(c-a\right)^5\) chia hết cho 30
Ta có a - b + b - c + c - a = 0 \(⋮30\)
=> (a - b) + (b - c) + (c - a) \(⋮\)30 (0)
Xét hiệu (a - b)5 + (b - c)5 + (c - a)5 - [(a - b) + (b - c) + (c - a)]
= [(a - b)5 - (a - b)] + [(b - c)5 - (b - c)] + [(c - a)5 - (c - a)]
Nhận thấy : (a - b)5 - (a - b) = (a - b)[(a - b)4 - 1]
= (a - b)[(a - b)2 - 1][(a - b)2 + 1]
= (a - b)[(a - b)2 - 1][(a - b)2 - 4 + 5]
= (a - b)[(a - b)2 - 1][(a - b)2 - 4] + 5(a - b)[(a - b)2 - 1]
= (a - b - 2)(a - b - 1)(a - b)(a - b + 1)(a - b + 2) + 5(a - b - 1)(a - b)(a - b + 1)
Nhận thấy (a - b - 2)(a - b - 1)(a - b)(a - b + 1)(a - b + 2) + 5(a - b - 1) \(⋮\)30 (tích 5 số nguyên liên tiếp) (1)
Lại có (a - b - 1)(a - b)(a - b + 1) \(⋮\)6
=> 5(a - b - 1)(a - b)(a - b + 1) \(⋮\)30 (2)
Từ (1) và (2) => (a - b - 2)(a - b - 1)(a - b)(a - b + 1)(a - b + 2) + 5(a - b - 1)(a - b)(a - b + 1) \(⋮\)30
=> (a - b)5 + (b - c)5 + (c - a)5 - [(a - b) + (b - c) + (c - a)] \(⋮\)30 (4)
Từ (0) ; (4) => (a - b)5 + (b - c)5 + (c - a)5 \(⋮\)30 (đpcm)
chứng minh rằng với mọi số nguyên a thì a^5-a luôn chia hết cho 5
Ta có : a5 _ a= a( a4 _ 1)= a(a2 _ 1)(a2 +1).
Nếu a\(⋮\)5 \(\Rightarrow\)a5 _ a = a(a2 _ 1)(a2 +1) \(⋮\)5 .Nếu a không chia hết cho 5 \(\Rightarrow\)a2 không chia hết cho 5 \(\Rightarrow\)a2 chia 5 dư 1 hoặc dư 4 ( Vì a2 là số chính phương).Nếu a2 chia 5 dư 1 \(\Rightarrow\) a2 _ 1\(⋮\)5 \(\Rightarrow\)a5 _ a = a( a2 _ 1)(a2 +1)\(⋮\)5Nếu a2 chia 5 dư 4 \(\Rightarrow\) a2 + 1\(⋮\)5 \(\Rightarrow\)a5 _ a = a( a2 _ 1)(a2 +1)\(⋮\)5Do đó : Với mọi a\(\in Z\)thì a5 _ a \(⋮\)5 (đpcm)
Đúng 0
Bình luận (0)
Bài 6
a, chứng minh rằng với mọi số tự nhiên n thuộc N thì 60n +15 chia hết cho 15 nhưng không chia hết cho 30
b, chứng minh rằng không có số tự nhiên nào chia 15 dư 6 , chia 9 dư 1
c, chứng minh rằng 1005a +2100b chia hết cho 15 , với mọi số tự nhiên a,b thuộc N
d, chứng minh rằng A= n2+n+1 không chia hết cho 2 và 5 với mọi số tự nhiên n thuộc N
a,60 chia hết cho 15 => 60n chia hết cho 15 ; 45 chia hết cho 15 => 60n+45 chia hết cho 15 (theo tính chất 1)
60n chia hết cho 30 ; 45 không chia hết cho 30 => 60n+45 không chia hết cho 30 (theo tính chất 2)
b,Giả sử có số a thuộc N thoả mãn cả 2 điều kiện đã cho thì a=15k+6 (1) và a=9q+1.
Từ (1) suy ra a chia hết cho 3, từ (2) suy ra a không chia hết cho 3. Đó là điều vô lí. Vậy không có số tự nhiên nào thoả mãn đề.
c,1005 chia hết cho 15 => 1005a chia hết cho 15 (1)
2100 chia hết cho 15 => 2100b chia hết cho 15 (2)
Từ (1) và (2) suy ra 1005a+2100b chia hết cho 15 (theo tính chất 1)
d,Ta có : n^2+n+1=nx(n+1)+1
nx(n+1) là tích của 2 số tự nhiên liên tiếp nên chia hết cho 2 suy ra nx(n+1)+1 là một số lẻ nên không chia hết cho 2.
nx(n+1) là tích của 2 số tự nhiên liên tiếp nên không có tận cùng là 4 hoặc 9 nên nx(n+1)+1 không có tận cùng là 0 hoặc 5, do đó nx(n+1)+1 không chia hết cho 5.
Đúng 0
Bình luận (0)
Mình xin trả lời ngắn gọn hơn! a)60 chia hết cho 15=> 60n chia hết cho 15 15 chia hết cho 15 =>60n+15 chia hết cho 15. 60 chia hết cho 30=>60n chia hết cho 30 15 không chia hết cho 30 =>60n+15 không chia hết cho 30 b)Gọi số tự nhiên đó là A Giả sử A thỏa mãn cả hai điều kiện => A= 15.x+6 & = 9.y+1 Nếu A = 15x +6 => A chia hết cho 3 Nếu A = 9y+1 => A không chia hết cho 3 => vô lí.=> c) Vì 1005;2100 chia hết cho 15=> 1005a; 2100b chia hết cho 15. => 1500a+2100b chia hết cho 15. d) A chia hết cho 2;5 => A chia hết cho 10. => A là số chẵn( cụ thể hơn là A là số có c/s tận cùng =0.) Nếu n là số chẵn => A là số lẻ. (vì chẵn.chẵn+chẵn+lẻ=lẻ) Nếu n là số lẻ => A là số lẻ (vì lẻ.lẻ+lẻ+lẻ=lẻ) => A không chia hết cho 2;5
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Chứng minh rằng : Với mọi số nguyên n thì \(n^5-n\) luôn chia hết cho 30
Câu hỏi của I lay my love on you - Toán lớp 8 - Học toán với OnlineMath dv
Đúng 0
Bình luận (0)
\(n^5-n=n\left(n^4-1\right)=n\left(n^2-1\right)\left(n^2+1\right)=n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)^{\left(1\right)}\)
\(=n\left(n-1\right)\left(n+1\right)\left(n^2-4+5\right)\)
\(=n\left(n-1\right)\left(n+1\right)\left[\left(n-2\right)\left(n+2\right)+5\right]\)
\(=\left(n-2\right)\left(n-1\right)n\left(n+1\right)\left(n+2\right)+5n\left(n-1\right)\left(n+1\right)\)
Vì n(n-2)(n+2)(n - 1)(n + 1) chia hết cho 5
5n(n - 1)(n + 1) chia hết cho 5
=> n(n-2)(n+2)(n - 1)(n + 1) + 5n(n - 1)(n + 1) chia hết cho 5
=> \(n^5-n⋮5\)(2)
Vì n , (n-1) , (n+1) là 3 số tự nhiên liên tiếp nên luôn tồn tại 1 số chia hết cho 2 và 3 trong 3 số này
Mà ( 2 ; 3 ) = 1
=> n(n+1)(n-1) chia hết cho 2.3=6
=> n(n+1)(n-1)(n²+1 ) chia hết cho 6
Hay n^5 - n chia hết cho 6 (3)
Từ (2) , (3) và ( 5 ; 6 ) = 1
=> n^5 -n chia hết cho 5.6 = 30
Vậy n^5 - n chia hết cho 30
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi số nguyên a và b thì ta có:
\(a.b\left(a^4-b^4\right)\)chia hết cho 30
Chứng minh rằng với mọi số nguyên a và b :
a, a3b - ab3 chia hết cho 6
b, a5b - ab5 chia hết cho 30

a)
b) đặt A=a^5b-ab^5=a(a^4b-b^5)=a(b(a^4-b^4))=ab... chia hết cho 2 (1)
+) Nếu a,b đồng du khi chia cho 3 thi a-b chia het cho 3 suy ra A chia het cho 3 (2)
+) Nếu a,b ko dong du khi chia cho 3 thi a+b chia het cho 3 suy ra Âchi het cho 3 (3)
Tu (2),(3) suy ra A luon chia het cho 3 (4)
Ma ab(a-b)(a+b)(a^2+b^2) chia het cho 5 (5)
Tu (1),(4),(5) suy ra A chia het cho 2;3;5 Vậy A chia het cho 30
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử bn ơi
Đúng 0
Bình luận (2)