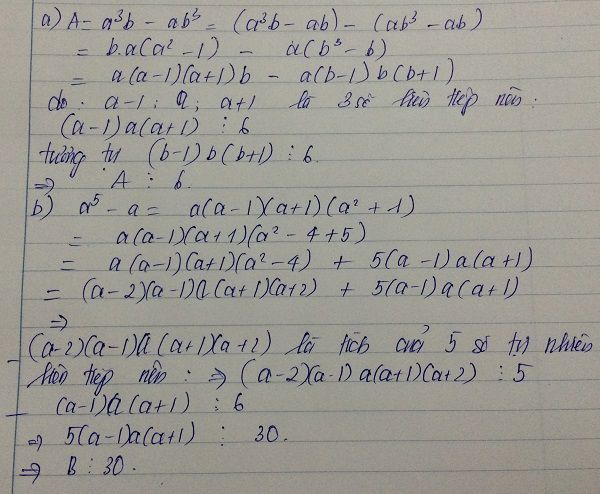a)
b) đặt A=a^5b-ab^5=a(a^4b-b^5)=a(b(a^4-b^4))=ab... chia hết cho 2 (1)
+) Nếu a,b đồng du khi chia cho 3 thi a-b chia het cho 3 suy ra A chia het cho 3 (2)
+) Nếu a,b ko dong du khi chia cho 3 thi a+b chia het cho 3 suy ra Âchi het cho 3 (3)
Tu (2),(3) suy ra A luon chia het cho 3 (4)
Ma ab(a-b)(a+b)(a^2+b^2) chia het cho 5 (5)
Tu (1),(4),(5) suy ra A chia het cho 2;3;5 Vậy A chia het cho 30
phân tích đa thức thành nhân tử bn ơi