a) Để A và n thuộc Z => n+1 chia hết cho n-2

A=(n-2+3) chia hết cho n-2

=> 3 chia hết cho n-2

lập bảng=> n thuộc {3,1,5,9,(-1)}

b) A lớn nhất khi n-2 nhỏ nhất=> n-2=1

                                           => n=3

Nhớ tk cho mk nha!

ĐKXĐ: \(x\ne\pm3\)

a

Khi x = 1:

\(A=\dfrac{3.1+2}{1-3}=\dfrac{5}{-2}=-2,5\)

Khi x = 2:

\(A=\dfrac{3.2+2}{2-3}=-8\)

Khi x = \(\dfrac{5}{2}:\)

\(A=\dfrac{3.2,5+2}{2,5-3}=\dfrac{9,5}{-0,5}=-19\)

b

Để A nguyên => \(\dfrac{3x+2}{x-3}\) nguyên

\(\Leftrightarrow3x+2⋮\left(x-3\right)\\3\left(x-3\right)+11⋮\left(x-3\right) \)

Vì \(3\left(x-3\right)⋮\left(x-3\right)\) nên \(11⋮\left(x-3\right)\)

\(\Rightarrow\left(x-3\right)\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\\ \Rightarrow x\left\{4;2;-8;14\right\}\)

c

Để B nguyên => \(\dfrac{x^2+3x-7}{x+3}\) nguyên

\(\Rightarrow x\left(x+3\right)-7⋮\left(x+3\right)\)

\(\Rightarrow-7⋮\left(x+3\right)\\ \Rightarrow x+3\inƯ\left\{\pm1;\pm7\right\}\)

\(\Rightarrow x=\left\{-4;-11;-2;4\right\}\)

d

\(\left\{{}\begin{matrix}A.nguyên.\Leftrightarrow x=\left\{-8;2;4;14\right\}\\B.nguyên\Leftrightarrow x=\left\{-11;-4;-2;4\right\}\end{matrix}\right.\)

=> Để A, B cùng là số nguyên thì x = 4.

54 nười 

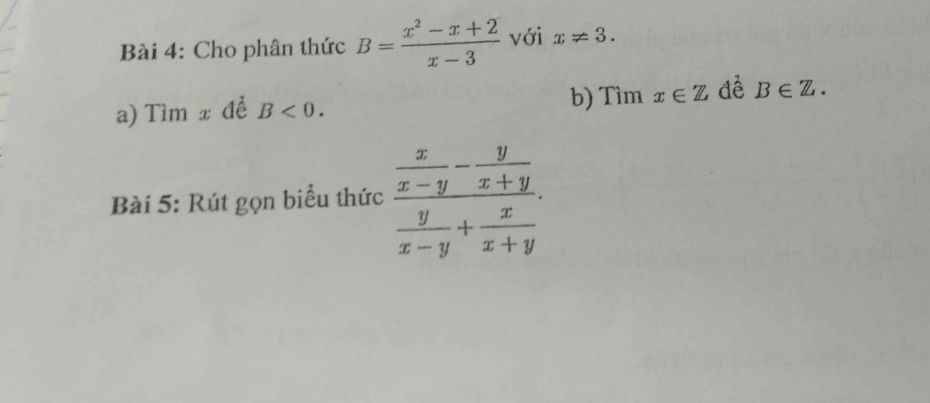
Bài 4:

a. Ta thấy: $x^2-x+2=(x-\frac{1}{2})^2+1,75>0$ với mọi $x$.

Do đó để $B=\frac{x^2-x+2}{x-3}<0$ thì $x-3<0$

$\Leftrightarrow x<3$ 

b. 

$B=\frac{x(x-3)+2(x-3)+8}{x-3}=x+2+\frac{8}{x-3}$

Với $x$ nguyên, để $B$ nguyên thì $x-3$ phải là ước của 8.

$\Rightarrow x-3\in\left\{\pm 1; \pm 2; \pm 4; \pm 8\right\}$

$\Rightarrow x\in \left\{4; 2; 5; 1; -1; 7; 11; -5\right\}$

Bài 5:

\(\frac{\frac{x}{x-y}-\frac{y}{x+y}}{\frac{y}{x-y}+\frac{x}{x+y}}=\frac{\frac{x(x+y)-y(x-y)}{(x-y)(x+y)}}{\frac{y(x+y)+x(x-y)}{(x-y)(x+y)}}\)

\(=\frac{x(x+y)-y(x-y)}{y(x+y)+x(x-y)}=\frac{x^2+y^2}{x^2+y^2}=1\)

a: Để B nguyên thì \(-7⋮x+3\)

\(\Leftrightarrow x+3\in\left\{1;-1;7;-7\right\}\)

hay \(x\in\left\{-2;-4;4;-10\right\}\)

b: Để A là số nguyên thì \(3x+2⋮x-3\)

\(\Leftrightarrow x-3\in\left\{1;-1;11;-11\right\}\)

hay \(x\in\left\{-2;-4;14;-8\right\}\)

Để A và B cùng là số nguyên thì \(x\in\left\{-2;-4\right\}\)

1.3+(-2)+x=5

-1+x=5

x=5-(-1)

x=6

Nhớ tick cho mình nha

\(A=\frac{x-13}{x+3}\inℤ\Leftrightarrow x-13⋮x+3\)

\(\Rightarrow x+3-16⋮x+3\)

      \(x+3⋮x+3\)

\(\Rightarrow16⋮x+3\)

tự làm tiếp!

b, \(A=\frac{x-13}{x+3}=\frac{x+3-16}{x+3}=\frac{x-3}{x-3}-\frac{16}{x+3}=1-\frac{16}{x+3}\)

để A đạt giá trị nhỏ nhất thì \(\frac{16}{x+3}\) lớn nhất

=> x+3 là số nguyên dương nhỏ nhất

=> x+3=1

=> x = -2

vậy x = -2 và \(A_{min}=1-\frac{16}{1}=-15\)

Ko bt

\(A=\frac{x+5}{x-4}=\frac{x-4+9}{x-4}=1+\frac{9}{x-4}\)

\(a)\)

\(\text{Để A có giá trị nguyên: }\)

\(\frac{9}{x-4}\in Z\)

\(x-4\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)

\(\rightarrow x\in\left\{1;3;\pm5;7;13\right\}\)

\(b)\)

\(\text{Để A có giá trị lớn nhất: }\)

\(\frac{9}{x-4}\)\(\text{lớn nhất}\)

\(x-4=1\)

\(x=5\)

\(c)\)

\(\text{Để A đạt giá trị nhỏ nhất:}\)

\(\frac{9}{x-4}\)\(\text{nhỏ nhất}\)

\(x-4=-1\)

\(x=3\)

Cho \(A=\frac{x+5}{x-4}=\frac{x-4+9}{x-4}=\frac{x-4}{x-4}+\frac{9}{x-4}=1+\frac{9}{x-4}\left(ĐK:x\in Z,x\ne4\right)\)

Để A nguyên \(\Rightarrow9⋮x-4\)hay \(x-4\inƯ\left(9\right)\)

Ta có \(x-4\inƯ\left(9\right)\in\left\{\pm1;\pm3;\pm9\right\}\)

\(\Rightarrow x\in\left\{5;3;7;1;13;-5\right\}\)

b, Đặt \(B=\frac{9}{x-4}\)\(\Rightarrow A_{max}\)khi \(B_{max}\)

Vì \(9>0\)để B đặt GTLN \(\Rightarrow\hept{\begin{cases}x-4>0\\\left(x-4\right)_{min}\end{cases}}\)

Mà \(x\in N\)\(\Rightarrow x-4=1\)

\(\Rightarrow x=5\)

\(\Rightarrow B_{max}=\frac{9}{5-4}=9\)

\(\Rightarrow A_{max}=1+9=10\)khi \(x=5\)

c, Đặt \(B=\frac{9}{x-4}\)\(\Rightarrow A_{min}\)khi \(B_{min}\)

Vì \(9>0\)để B đạt GTNN \(\Rightarrow\hept{\begin{cases}x-4< 0\\\left(x-4\right)_{max}\end{cases}}\)

Mà \(x\in N\)\(\Rightarrow x-4\in Z\)

\(\Rightarrow x-4=-1\)

\(\Rightarrow x=3\)

\(\Rightarrow B_{min}=\frac{9}{3-4}=-9\)

\(\Rightarrow A_{min}=1+\left(-9\right)=\left(-8\right)\)khi \(x=3\)