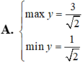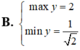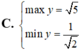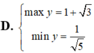tìm min max của hàm số lượng giác 𝑦=sin𝑥+0.2cos𝑥
HD
Những câu hỏi liên quan
tìm tập xác định của hàm số: 𝑦=√(1+sin𝑥)/(1−sin𝑥).
giúp mình với ạ.!!
ĐKXĐ: \(sinx\ne1\Rightarrow x\ne\frac{\pi}{2}+k2\pi\)
(Không cần tìm điều kiện cho căn thức vì biểu thức luôn không âm)
Đúng 0
Bình luận (0)
Tìm min, max của hàm số lượng giác
\(y=\sqrt{4-2\sin^52x}-8\)
Ta có:
\(-1\le\sin2x\le1\)
=> \(\sqrt{4-2.\left(1\right)^5}-8\le\sqrt{4-2.\left(\sin2x\right)^5}-8\le\sqrt{4-2.\left(-1\right)^5}-8\)
=> \(\sqrt{2}-8\le\sqrt{4-2.\left(\sin2x\right)^5}-8\le\sqrt{6}-8\)
=> tìm ddc min và max
Bài 1. Cho 2 hàm số 𝑦 𝑦 −𝑥/2 + 3 và 𝑦 𝑥 − 2a) Vẽ đồ thị 2 hàm số trên cùng một hệ trục tọa độ.b) Tìm tọa độ giao điểm của đồ thị 2 hàm số.c) Viết phương trình đường thẳng (𝐷): 𝑦 𝑎𝑥 + 𝑏 biết (𝐷) song song với 𝑦 -𝑥/2 + 3 và đi qua 𝑀(4;5).Bài 2. Cho 2 đường thẳng (𝑑1): 𝑦 𝑥/2 − 2 và (𝑑2): 𝑦 𝑥 − 2a) Vẽ (𝑑1) và (𝑑2) trên cùng một hệ trục tọa độ.b) Tìm tọa độ giao điểm của đồ thị 2 hàm số.c) Viết phương trình đường thẳng (𝐷): 𝑦 𝑎𝑥 + 𝑏 biết (𝐷) song song với (𝑑2) và cắt (𝑑1) tại điểm có hoành độ...
Đọc tiếp
Bài 1. Cho 2 hàm số 𝑦 = 𝑦 = −𝑥/2 + 3 và 𝑦 = 𝑥 − 2
a) Vẽ đồ thị 2 hàm số trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của đồ thị 2 hàm số.
c) Viết phương trình đường thẳng (𝐷): 𝑦 = 𝑎𝑥 + 𝑏 biết (𝐷) song song với 𝑦 = -𝑥/2 + 3 và đi qua 𝑀(4;5).
Bài 2. Cho 2 đường thẳng (𝑑1): 𝑦 = 𝑥/2 − 2 và (𝑑2): 𝑦 = 𝑥 − 2
a) Vẽ (𝑑1) và (𝑑2) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của đồ thị 2 hàm số.
c) Viết phương trình đường thẳng (𝐷): 𝑦 = 𝑎𝑥 + 𝑏 biết (𝐷) song song với (𝑑2) và cắt (𝑑1) tại điểm có hoành độ là 2.
Bài 3. Cho hàm số y = -x + 5 có đồ thị là (D1)
a) Vẽ (D1).
b) Viết phương trình đường thẳng (D2) song song với (D1) và cắt trục tung tại điểm có tung độ là 3.
Bài 4. Cho (D): y = -x/2 + 3
a) Vẽ (D) trên hệ trục tọa độ.
b) Viết phương trình đường thẳng (D') song song với (D) và cắt trục hoành tại điểm có hoành độ bằng -2.
Bài 5. Cho hàm số 𝑦 = 2𝑥 + 3 có đồ thị (d).
a) Vẽ đồ thị (d) của hàm số trên.
b) Gọi A, B lần lượt là giao điểm của (d) với Ox, Oy. Tính diện tích tam giác OAB.
Bài 6. Cho 3 đường thẳng (𝑑1): 𝑦= 3𝑥, (𝑑2): 𝑦 = 𝑥 + 2, (𝑑3): 𝑦= ( 𝑚 − 3 ) 𝑥 + 2𝑚 + 1. Tìm m để 3 đường thẳng đồng quy.
Bài 7. Để đổi nhiệt độ F (Fahrenheit) sang độ C (Celsius) ta dùng công thức 𝐶 = 5/9(𝐹 − 32)
a) C có phải là hàm số bậc nhất của biến số F không?
b) Hãy tính C khi F = 30.
c)Hãy tính F khi C = 25.
Bài 8. Năm 1990 diện tích rừng trên Trái Đất là 718,3 hecta . Theo số liệu thống kế người ta nhận thấy rằng, kể từ năm 1990 thì mỗi năm diện tích rừng nhiệt đới trên Trái Đất giảm đi khoảng 4,6 triệu hecta . Gọi S là diện tích rừng trên Trái Đất, t là số năm kể từ năm 1990.
a) Hãy biểu thị S theo t và cho biết S có phải là hàm số bậc nhất theo biến t không?
b) Tính diện tích rừng trên Trái Đất vào năm 2022.
Bài 9. Tại bề mặt đại dương, áp suất nước bằng áp suất khí quyển và là 1 atm ( atmosphere ). Bên dưới mặt nước, áp suất tăng thêm 1 atm cho mỗi 10 mét sâu xuống. Biết rằng mối liên hệ giữa áp suất y ( atm ) và độ sâu x ( m ) dưới mặt nước là một hàm số bậc nhất có dạng 𝑦 = 𝑎𝑥 + 𝑏
a) Xác định hệ số a, b.
b) Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất là 2,85 atm?
( Trích đề thi vào lớp 10 TP.HCM 2019 –2020 )
Bài 10. Nhiệt độ sôi của nước không phải lúc nào cũng là 100 độ 𝐶 mà phụ thuộc vào độ cao của nơi đó so với mực nước biển. Chẳng hạn TP.HCM có độ cao xem như ngang mực nước biển ( x = 0m ) thì nước có nhiệt độ sôi là 𝑦 = 100 độ 𝐶 nhưng ở thủ đô La Paz của Bolivia, Nam Mỹ có độ cao 𝑥 = 3600𝑚 so với mực nước biển thì nhiệt độ sôi của nước là 𝑦 =87 độ 𝐶. Ở độ cao khoảng vài km, người ta thấy mỗi liên hệ giữa 2 đại lương này là một hàm số bậc nhất 𝑦 = 𝑎𝑥 + 𝑏 có đồ thị như sau:
a) Xác định hệ số a, b.
b) Thành phố Đà Lạt có độ cao 1500m so với mực nước biển. Hỏi độ sôi của nước ở thành phố này là bao nhiêu?
Bài 11. Nếu bỏ qua sự phụ thuộc về vĩ độ thì sự thay đổi nhiệt độ không khí tùy theo độ cao của địa hình: cứ lên cao 100 mét thì nhiệt độ không khí giảm xuống 0,6 độ C. Thành phố Hồ Chí Minh có độ cao bằng mực nước biển ( độ cao 0 mét ). Thành phố Đà Lạt có độ cao 1500 mét so với mực nước biển. Gọi x ( độ C ) là nhiệt độ không khí tại Thành phố Hồ Chí Minh và y ( độ C ) là nhiệt độ không khí tại Thành phố Đà Lạt.
a) Hãy lập công thức tính y theo x.
b) Khi Thành phố Đà Lạt có nhiệt độ là 15 độ C thì Thành phố Hồ Chí Minh có nhiệt độ là bao nhiêu?
MẤY BẠN GIÚP MÌNH BAO NHIÊU CÂU CŨNG ĐƯỢC Ạ!
MÌNH CẢM ƠN TRƯỚC Ạ!
MUCH LOVE!
Bài 1:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-\dfrac{1}{2}x+3=x-2\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{2}x=5\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10}{3}\\y=\dfrac{10}{3}-2=\dfrac{4}{3}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
mn cho tui hỏi cái
tìm min max của |f(x)| ý
sao Max lại tìm theo 2TH còn min lại tìm theo so sánh trên dưới với trục ox vậy
tai sao lại không thể làm theo cách của tìm max
dạng mà tìm tham số m để hàm số |f(x)| có Min/Max trên [a,b] ý
Tìm Min, Max của hàm số:
\(y=\sqrt{sinx}+\sqrt{cosx}\)
ĐKXĐ: \(sinx;cosx\ge0\)
Do \(\left\{{}\begin{matrix}0\le sinx\le1\\0\le cosx\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\sqrt{sinx}\ge sin^2x\\\sqrt{cosx}\ge cos^2x\end{matrix}\right.\)
\(\Rightarrow\sqrt{sinx}+\sqrt{cosx}\ge sin^2x+cos^2x=1\)
\(\Rightarrow y_{min}=1\) (khi \(x=\dfrac{\pi}{2}+k2\pi\) hoặc \(k2\pi\))
Mặt khác áp dụng Bunhiacopxki:
\(y\le\sqrt{2\left(sinx+cosx\right)}\le\sqrt{2\sqrt{2\left(sin^2x+cos^2x\right)}}=\sqrt[4]{8}\)
\(y_{max}=\sqrt[4]{8}\) khi \(x=\dfrac{\pi}{4}+k2\pi\)
Đúng 1
Bình luận (0)
Tìm GTLN (max); GTNN (min) của hàm số
y
2
x
+
1
+
4
-
x
.
Đọc tiếp
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .
Tìm GTLN (max), GTNN (min) của hàm số
y
x
+
2
x
với
x
∈
1
;
3
Đọc tiếp
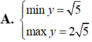
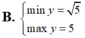
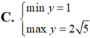
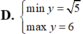
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x với x ∈ 1 ; 3
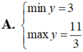
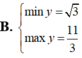
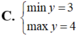
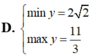
Tìm GTLN (max), GTNN (min) của hàm số
y
x
2
-
3
x
-
2
trên
5
2
;
5
Đọc tiếp
Tìm GTLN (max), GTNN (min) của hàm số y = x 2 - 3 x - 2 trên 5 2 ; 5
Tìm GTLN (max), GTNN (min) của hàm số
y
x
+
2
x
2
+
1
trên
-
1
;
1
Đọc tiếp
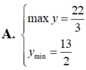
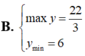
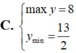
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x 2 + 1 trên - 1 ; 1
