cho 3 điểm C,D,E thẳng hàng . Biết CE=DE=2cm.chứng tỏ E là trung điểm của CD
TG
Những câu hỏi liên quan
cho ba điểm C,D,I thẳng hàng .biết CI =2cm;DI=2cm.chứng tỏ rằng I là trung điểm của CD
Vì CI=DI(=2cm) nên điểm I nằm giữa 2 điểm C và D
Có : CI=DI(=2cm)
Điểm I nằm giữa 2 điểm C và D
Vậy điểm I là trung điểm của CD
Ta có :
CI = DI = (2cm) và CI + DI = CD = 2 + 2 = 4 (cm)
Ở đây ta thấy I nằm giữa hai điểm C và D ( CI + DI = CD | 2 + 2 = 4 ) và cách đều C và D ( CI = DI ) . Vậy I là trug điểm của CD .
Cho đoạn thẳng AB = 4cm . Gọi O là trung điểm của AB.Trên tia OA lấy điểm E , trên tia OB lấy điểm F sao cho DE = OF= 2cm.Chứng tỏ rằng AE=BF
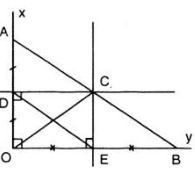
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, đường trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng :
a) CE = OD
b) \(CE\perp CD\)
c) CA = CB
d) CA // DE
e) Ba điểm A, B, C thẳng hàng
c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).
Đúng 0
Bình luận (0)
c) Chứng minh CA = CB
- Vì C nằm trên đường trung trực của OA nên CA = CO (3)
- Vì C nằm trên đường trung trực của OB nên CB = CO (4)
Từ (3) và (4) suy ra: CA = CB (đpcm).
Đúng 0
Bình luận (0)
các bn ơi cx câu hỏi này các bn cm dùm mình: tam giác odc=tam giác ceo đi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Mấy bn cho mk hỏi bt này giải sao? giúp mk vs nha mk đag gấp thanks nhìu 3Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, Đường trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của 2 đường trung trực đó. CM rằng:a. CEODb. CE vuông góc CDc. CACBd. CA song song DEe. 3 điểm A, B, C thẳng hàng
Đọc tiếp
Mấy bn cho mk hỏi bt này giải sao? giúp mk vs nha mk đag gấp thanks nhìu <3
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, Đường trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của 2 đường trung trực đó. CM rằng:
a. CE=OD
b. CE vuông góc CD
c. CA=CB
d. CA song song DE
e. 3 điểm A, B, C thẳng hàng
Trên tia đối của tia AN lấy điểm E sao cho AE=2cm.Chứng tỏ A là trung điểm của đoạn thẳng HE
Cho góc vuông xoy, điểm A thuộc tia Ox, điểm B thuộc tia Oy.Đường trung trực của OA cắt Ox ở D,đường trung trực của OB cắt Oy ở E.Gọi C là giao điểm 2 đường trung trực đó.Chứng minh:
a) CE=OD
b)CE vuông góc CD
c)CA=CB
d)CA//DE
e) 3 điểm B A C thẳng hàng
Cho tam giác ABC cân đỉnh A . Trên cạnh AB lấy điểm D , trên tia đối của tia CA lấy điểm E sao cho BD = CE . Nối D với E . Gọi I là trung điểm của đoạn thẳng DE . Chứng minh rằng ba điểm B , I , C thẳng hàng
kẻ DK//CE
góc DKB=góc ACB
=>góc DKB=góc DBK
=>DK=DB=CE
Xét tứ giác DKEC có
DK//EC
DK=EC
=>DKEC là hình bình hành
=>DE cắt KC tại trung điểm của mỗi đường
=>I là trung điểm của KC
=>B,I,C thẳng hàng
Đúng 1
Bình luận (0)
Cho góc vuông xOy, điểm A thuộc tia Ox,điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox tại D, đường trung trực của đoạn OB cắt Oy tại E. Gọi C là giao điểm của hai đường trung trực đó. Chứng mình rằng:
a) CE = OD
b) CE vuông góc với CD
c) CA = CB
d) CA song song với DE
e) Ba điểm A, B, C thẳng hàng
a) OD // CE (_|_ OE) và CD // OE (_|_OD)
=> ODCE là hình bình hành . Mà O^ = 90o
=> ODCE là hình chữ nhật (*) => CE=OD
b) (*) => DCE^ = 90o hay CE_|_ CD
c) tam giác ADC và tam giác CEB:
AD = CE (=DO)
EDC^ = CEB^ = 90o
DC=EB (=OE)
=> tam giác ADC= tam giác CEB (2 cạnh góc vuông)
=> AC = CB ( 2 cạnh tương ứng)
d) AD //= CE (cmt) => tứ giác ACED là hình bình hành => AC // DE (*)
e) DC //= EB => tứ giác DCBE là hình bình hành
=> DE//BC ( 2 cạnh đối) (**)
Từ (*) và (**) => A,C,B thẳng hàng
Đúng 0
Bình luận (0)
CHO 1 ĐOẠN THẲNG CD VÀ 1 ĐIỂM E NẰM GIỮA CD .GỌI IK LẦN LƯỢT LÀ TRUNG ĐIỂM CỦA CE VÀ DE .TÍNH CD BIẾT IK =4CM