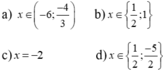4x2 + 8x + 12 = 8
NH
Những câu hỏi liên quan
x3-4x2+8x-8
=(x3-4x2+8x-4)-4
giải tiếp hộ mik vs
\(x^3-4x^2+8x-8\)
\(=x^3-2x^2+4x-2x^2+4x-8\)
\(=\left(x^3-2x^2+4x\right)-\left(2x^2-4x+8\right)\)
\(=x\left(x^2-2x+4\right)-2\left(x^2-2x+4\right)\)
\(=\left(x^2-2x+4\right)\left(x-2\right)\)
Đúng 3
Bình luận (2)
Giải các phương trình sau:a)
x
−
1
2
−
2
x
+
5
2
0
;
b)
x
2
−
1
−
x
2...
Đọc tiếp
Giải các phương trình sau:
a) x − 1 2 − 2 x + 5 2 = 0 ;
b) x 2 − 1 − x 2 − 2 x − 1 2 = 0 ;
c) x 3 + 8 = − 2 x x + 2 ;
d) 4 x 2 + 8 x − 5 = 0 .
(8x+12-4X2):(x-3)
\(\left(8x+12-4x^2\right):\left(x-3\right)=\left[4x\left(x-3\right)+20\left(x-3\right)+72\right]:\left(x-3\right)=\left[\left(x-3\right)\left(4x+20\right)+72\right]:\left(x-3\right)=4x+20R72\)
Đúng 1
Bình luận (1)
x3-4x2+8x-8
\(x^3-4x^2+8x-8\\ =x^3-2x^2+4x-2x^2+4x-8\\ =x\left(x^2-2x+4\right)-2\left(x^2-2x+4\right)\\ =\left(x-2\right)\left(x^2-2x+4\right)\)
Đúng 2
Bình luận (0)
Để giải phương trình đa thức x^3 - 4x^2 + 8x - 8, ta có thể sử dụng phương pháp nhân thức tìm nghiệm.
Đầu tiên, ta kiểm tra x = 1 có phải là nghiệm của phương trình hay không bằng cách thay x = 1 vào phương trình:
(1)^3 - 4(1)^2 + 8(1) - 8 = 1 - 4 + 8 - 8 = -3
Vì kết quả không bằng 0, nên x = 1 không phải là nghiệm của phương trình.
Tiếp theo, ta sử dụng phương pháp chia đa thức để tìm nghiệm. Ta chia đa thức x^3 - 4x^2 + 8x - 8 cho (x - 2) bằng cách sử dụng phép chia đa thức.
x^2 - 2x + 4x - 2 | x^3 - 4x^2 + 8x - 8 - (x^3 - 2x^2) --------------- -2x^2 + 8x + ( -2x^2 + 4x) --------------- 4x - 8 - (4x - 8) ------------ 0
Khi chia x^3 - 4x^2 + 8x - 8 cho (x - 2), ta thu được kết quả là x^2 - 2x + 4.
Vậy phương trình có thể viết lại dưới dạng:
(x - 2)(x^2 - 2x + 4) = 0
Để tìm các nghiệm của phương trình, ta giải các đa thức nhỏ hơn.
Từ x^2 - 2x + 4 = 0, ta có thể sử dụng công thức giải phương trình bậc hai:
x = (2 ± √(2^2 - 4(1)(4))) / (2(1)) = (2 ± √(-12)) / 2 = (2 ± 2i√3) / 2 = 1 ± i√3
Vậy phương trình có 3 nghiệm là x = 2, x = 1 + i√3 và x = 1 - i√3.
Đúng 0
Bình luận (0)
tìm x
x6 +2x3+1=0
x(x-5)=4x-20
x4-2x2=8-4x2
(x3-x2)-4x2+8x-4=0
\(x^6+2x^3+1=0\)
\(\Leftrightarrow\left(x^3\right)^2+2x^3+1=0\)
\(\Leftrightarrow\left(x^3+1\right)^2=0\)
\(\Leftrightarrow x^3=\left(-1\right)^3\)
\(\Leftrightarrow x=-1\)
___________
\(x\left(x-5\right)=4x-20\)
\(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
_____________
\(x^4-2x^2=8-4x^2\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(4x^2-8\right)=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+4\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x^2-2\right)\left(x^2+4\right)=0\)
\(\Leftrightarrow x^2=2\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
_______________
\(\left(x^3-x^2\right)-4x^2+8x-4\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
8. x3 - 4x2 +8x- 32 = 0
9. x3 +27+(x+3)(x-9) = 0
10. x² -10x +16 = 0
11. 2x2 + 3(x-1)(x+1)=5x(x+1)
12. (х+3)(х-3)-(х-2)(х+5)=0
bài 3 phân tích đa thức sau thành nhân tử
a 4x2 -16 + (3x +12) (4-2x)
b x3 + X2Y -15x -15y
c 3(x+8) -x2 -8x
d x3 -3x2 + 1 -3x
e 5x2 -5y2 -20x + 20y
kkk =0)
a) \(4x^2-16+\left(3x+12\right)\left(4-2x\right)\)
\(=\left(2x-4\right)\left(2x+4\right)-3\left(x+4\right)\left(2x-4\right)\)
\(=\left(2x-4\right)\left(2x+4-3x-12\right)\)
\(=-\left(2x-4\right)\left(x+8\right)\)
b) \(x^3+x^2y-15x-15y\)
\(=x^2\left(x+y\right)-15\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-15\right)\)
c) \(3\left(x+8\right)-x^2-8x\)
\(=3\left(x+8\right)-x\left(x+8\right)\)
\(=\left(x+8\right)\left(3-x\right)\)
d) \(x^3-3x^2+1-3x\)
\(=x^3+1-3x^2-3x\)
\(=\left(x+1\right)\left(x^2-x+1\right)-3x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-x+1-3x\right)\)
\(=\left(x+1\right)\left(x^2-4x+1\right)\)
d) \(5x^2-5y^2-20x+20y\)
\(=5\left(x^2-y^2\right)-20\left(x-y\right)\)
\(=5\left(x-y\right)\left(x+y\right)-20\left(x-y\right)\)
\(=5\left(x-y\right)\left(x+y-4\right)\)
Đúng 2
Bình luận (0)
Biết rằng phương trình
4
x
2
-
1
2
8
x
+
1
có nghiệm lớn nhất là
x
0
. Chọn khẳng định đúng A.
x
0
3 B.
x...
Đọc tiếp
Biết rằng phương trình 4 x 2 - 1 2 = 8 x + 1 có nghiệm lớn nhất là x 0 . Chọn khẳng định đúng
A. x 0 = 3
B. x 0 < 2
C. x 0 > 1
D. x 0 < 0
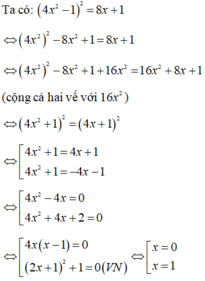
Tập nghiệm của phương trình là S = {0; 1}
Suy ra nghiệm lớn nhất của phương trình là x 0 = 1 < 2
Đáp án cần chọn là B
Đúng 0
Bình luận (0)
Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x?
a) 8x > 4x ; b) 4x > 8x
c) 8x2 > 4x2 ; d) 8 + x > 4 + x
a) Ta có: 8 > 4 nên để 8x > 4x thì x > 0
Do đó, chỉ đúng khi x > 0 (hay nói cách khác nếu x < 0 thì a sai)
b) Ta có: 4 < 8 nên để 4x > 8x thì x < 0 .
Do đó, khẳng định chỉ đúng khi x < 0
c) chỉ đúng khi x ≠ 0
d) Ta có: 8 > 4 nên với mọi x thì 8+ x > 4+ x ( tính chất cộng hai vế của BĐT với 1 số)
Do đó, khẳng định đúng với mọi x.
Vậy khẳng định d là đúng với mọi giá trị của x.
Đúng 0
Bình luận (0)
Giải BPT
a, x2 - 2x + 8 < 0
b, 4x2 - 4x - 8 > 0
c, (2x - 3)/(19 + 8x) < 0
d, (x - 2)/(x - 1) - 3/(x - 1) < 1