Vẽ 4 điểm : A ; B ; C ; D trên 1 đường thẳng sao cho điểm B nằm giữa 2 điểm : A ; C và điểm C nằm giữa điểm : B ; D. Sau đó hãy kể tên : các tia, các cặp đối nhau, các cặp tia phân biệt, các cặp tia trùng nhau có trong hình vẽ đó.
TN
Những câu hỏi liên quan
a/ hãy vẽ 10 điểmthành 5 hàng mỗi hàng có 4 điểm
b/ hãy vẽ 7 điểm thành 6 hàng mỗi hàng có 3 điểm
c/hãy vẽ 12 điểm có 6 hàng mỗi hàng có 4 điểm
ukm bn ưiiiiiiiii
vẽ 4 điểm A,B,C,D sao cho 3 điểm A,B,C thẳng hàng 3 điểm B,C,D thẳng hàng.Giai thích cách vẽ
dùng thước vạch 1 đường thẳng . chấm 4 điểm A,B,C,D trên đường thẳng đó.
Đúng 0
Bình luận (0)
Vẽ đường thẳng đi qua 4 điểm A,B,C,D
Vẽ điểm Q không thuộc đường thẳng DC
Vẽ tiếp các cặp điểm đi qua các điểm
Cho 4 điểm A,B,C,D.Qua 2 trong 4 điểm đó ta vẽ 1 đoạn thẳng . Hãy vẽ hình và nêu tên khi :
a) Có 3 điểm thẳng hàng
b) Không có 3 điểm nào thẳng hàng
Bài 4: (3,0 điểm)a) Vẽ hình theo diễn đạt sau:- Vẽ đường thẳng m đi qua 2 điểm A và B.- Vẽ đường thẳng d cắt đường thẳng m tại điểm C nằm giữa A và B.- Lấy điểm D thuộc đường thẳng m sao cho D và B nằm cùng phía đối với điểm C- Qua D vẽ đường thẳng n cắt đường thẳng d tại điểm I.- Vẽ tia IA, IB.b) Đọc tên các tia gốc Bc) Vẽ hình chữ nhật có chiều dài 4cm, chiều rộng 3cm. Chỉ ra trục đối xứng, tâmđối xứng của nó (nếu có).Cứu với!!!
Đọc tiếp
Bài 4: (3,0 điểm)
a) Vẽ hình theo diễn đạt sau:
- Vẽ đường thẳng m đi qua 2 điểm A và B.
- Vẽ đường thẳng d cắt đường thẳng m tại điểm C nằm giữa A và B.
- Lấy điểm D thuộc đường thẳng m sao cho D và B nằm cùng phía đối với điểm C
- Qua D vẽ đường thẳng n cắt đường thẳng d tại điểm I.
- Vẽ tia IA, IB.
b) Đọc tên các tia gốc B
c) Vẽ hình chữ nhật có chiều dài 4cm, chiều rộng 3cm. Chỉ ra trục đối xứng, tâm
đối xứng của nó (nếu có).
Cứu với!!!
b: Các tia gốc B là Bm,BD

Trục đối xứng của hình chữ nhật ABCD là MN,EF
Tâm đối xứng của hình chữ nhật ABCD là O
Đúng 0
Bình luận (0)
Vẽ 3 điểm A,B,C thuộc đường thẳng d. Vẽ điểm K ko thuộc đường thẳng d. Vẽ các đường thẳng đi qua các cặp trong 4 điểm trên
Cho 4 điểm A,B,C,D trong đó ko có 3 điểm nào thẳng hàng . Cứ qua 2 điểm vẽ 1 đoạn thẳng . Hỏi vẽ được tất cả bao nhiêu đoạn thẳng ? Là những đoạn thẳng nào ? Kết quả có thay đổi ko nếu 4 điểm A,B,C,D thẳng hàng ( vẽ hình )
TH1 : ( không có 3 điểm nào thẳng hàng)
Số đoạn thẳng là : 4 . ( 4 -1 ) / 2 = 4.3/2 = 6
TH2 : ( bốn điểm thẳng hàng )
, , , ,
Số đoạn thẳng là :
4 . ( 4 - 1) / 2 = 6 (đoạn thẳng)
* Chỉ có đường thẳng mới thay đổi khi có từ 3 điểm thẳng hàng thôi còn đoạn thẳng thì không thay đổi nhé.
Đúng 0
Bình luận (0)
Cho em hỏi ba câu này ạ: a. Vẽ được 6 đường thẳng mà mỗi đường thẳng đi qua 2 trong 4 điểm trên b. Vẽ được 4 đường thẳng mà mỗi đường thẳng đi qua 2 trong 4 điểm trên c. Vẽ được 2 đường thẳng mà mỗi đường thẳng đi qua 2 trong 4 điểm trên
Để vẽ được các đường thẳng như yêu cầu, chúng ta có thể sử dụng nguyên tắc "mỗi đường thẳng đi qua 2 trong 4 điểm trên".
a. Để vẽ 6 đường thẳng, ta có thể chọn 2 điểm từ 4 điểm trên và vẽ đường thẳng đi qua chúng. Vì có 4 điểm, ta có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 6 đường thẳng.
b. Tương tự, để vẽ 4 đường thẳng, ta có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 4 đường thẳng.
c. Để vẽ 2 đường thẳng, ta cũng có C(4,2) = 6 cách chọn 2 điểm từ 4 điểm trên. Vậy, ta có thể vẽ được 2 đường thẳng.
Với các yêu cầu trên, chúng ta có thể vẽ được số đường thẳng tương ứng.
Đúng 0
Bình luận (0)
Cho năm điểm A,B,C,D,E. Biết rằng qua 4 điểm A,B,C,D có thể vẽ được một đường tròn. Qua 4 điểm B,C,D,E cũng vẽ được 1 đường tròn. Chứng minh rằng cả 5 điểm cùng thuộc một đường tròn.
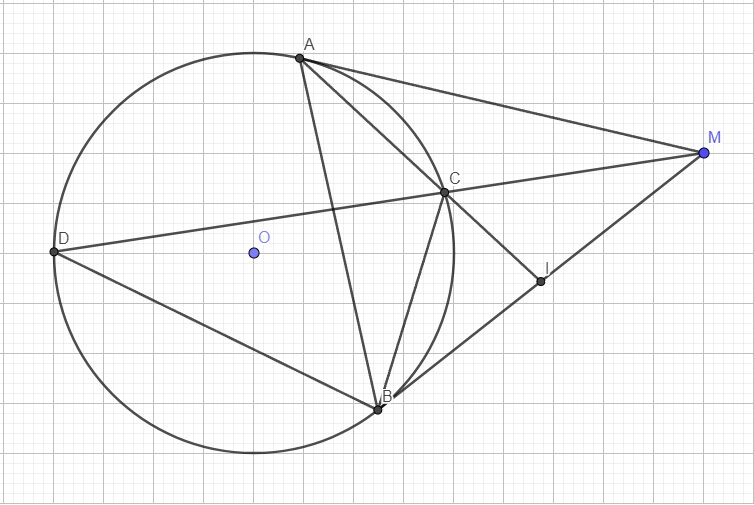
Từ điểm M nằm ngoài (O) vẽ hai tiếp tuyến MA, MB (A,B là tiếp điểm) a) Chứng minh 4 điểm M,A,O,B cùng thuộc một đường tròn b) Vẽ I là trung điểm MB. Nối AI cắt (O) tại C. Chứng minh IB²=IC.IA c) MC cắt (O) tại D. Chứng minh MB²= MC.MD Suy ra MC.MD=IC.IA
a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{IBC}\) là góc tạo bởi tiếp tuyến BI và dây cung BC
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{IBC}=\widehat{BAC}\)
Xét ΔIBC và ΔIAB có
\(\widehat{IBC}=\widehat{IAB}\)
\(\widehat{BIC}\) chung
Do đó: ΔIBC~ΔIAB
=>\(\dfrac{IB}{IA}=\dfrac{IC}{IB}\)
=>\(IB^2=IA\cdot IC\)
c: Xét (O) có
\(\widehat{MBC}\) là góc tạo bởi tiếp tuyến BM và dây cung BC
\(\widehat{CDB}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{MBC}=\widehat{CDB}\)
Xét ΔMBC và ΔMDB có
\(\widehat{MBC}=\widehat{MDB}\)
\(\widehat{BMC}\) chung
Do đó: ΔMBC~ΔMDB
=>\(\dfrac{MB}{MD}=\dfrac{MC}{MB}\)
=>\(MB^2=MD\cdot MC\)
Đúng 2
Bình luận (0)
a. Em tự giải
b.
Ta có: IB là tiếp tuyến (O) tại B nên \(\widehat{BAC}=\widehat{CBI}\) (góc nội tiếp và góc tạo bởi tiếp tuyến - dây cung cùng chắn BC)
Xét hai tam giác ABI và BCI có:
\(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{CBI}\left(cmt\right)\\\widehat{BIA}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta ABI\sim\Delta BCI\left(g.g\right)\)
\(\Rightarrow\dfrac{IA}{IB}=\dfrac{IB}{IC}\Rightarrow IB^2=IC.IA\)
c.
Ta có \(\widehat{BDC}\) và \(\widehat{MBC}\) là góc nội tiếp và góc tạo bởi tiếp tuyến sây cung cùng chắn BC
\(\Rightarrow\widehat{BDC}=\widehat{MBC}\)
Xét hai tam giác MBD và MCB có:
\(\left\{{}\begin{matrix}\widehat{BMD}\text{ chung}\\\widehat{BDC}=\widehat{MBC}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBD\sim\Delta MCB\left(g.g\right)\)
\(\Rightarrow\dfrac{MB}{MC}=\dfrac{MD}{MB}\Rightarrow MB^2=MC.MD\)
Đẳng thức cuối em ghi sai.
Do I là trung điểm MB \(\Rightarrow MB=2IB\Rightarrow MB^2=4IB^2\)
\(\Rightarrow MC.MD=4IC.IA\) (đây mới là đẳng thức đúng)
Đúng 3
Bình luận (0)