Cho x , y , z là 3 số dương thỏa mãn 4x + 9y + 16z = 49 CMR: T = 1/x + 25/y + 64/z \(\ge49\)
cho x,y,z>0 thỏa mãn 4x+9y+16z=49. CM\(\frac{1}{x}+\frac{25}{y}+\frac{64}{z}\ge49\)
Ta có:
\(\left(4x+9y+16z\right)\left(\frac{1}{x}+\frac{25}{y}+\frac{64}{z}\right)\ge\left(\sqrt{\frac{4x}{x}}+\sqrt{\frac{9y.25}{y}}+\sqrt{\frac{16z.64}{z}}\right)^2\)
\(\Leftrightarrow49\left(\frac{1}{x}+\frac{25}{y}+\frac{64}{z}\right)\ge\left(2+15+32\right)^2\)
\(\Leftrightarrow\frac{1}{x}+\frac{25}{y}+\frac{64}{z}\ge49\)
Dấu = xảy ra tại \(x=\frac{1}{2};y=\frac{5}{3};z=2\)
Cho x, y, z là ba số dương thỏa mãn 4x+9y+16z=49. Giá trị nhỏ nhất của biểu thức \(A=\frac{1}{x}+\frac{25}{y}+\frac{64}{z}\)
Cho x,y,z là 3 số thực dương và thỏa mãn: 4x^2 + 9y^2 + 16z^2 = 1.Tìm giá trị nhỏ nhất của A = 2x / (9y^2 + 16z^2) + 3y / (4x^2 + 16 z^2) + 4z / (4x^2 + 9y^2)
Cho x, y, z là các số thực thỏa mãn điều kiện 4 x + 9 y + 16 z = 2 x + 3 y + 4 z . Tìm giá trị lớn nhất của biểu thức T = 2 x + 1 + 3 y + 1 + 4 z + 1
A. 13 + 87 2
B. 11 + 87 2
C. 7 + 37 2
D. 9 + 87 2
Cho x, y, z là các số thực thỏa mãn điều kiện 4 x + 9 y + 16 z = 2 x + 3 y + 4 z . Tìm giá trị lớn nhất của biểu thức T = 2 x + 1 + 3 y + 1 + 4 z + 1
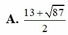
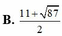
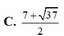
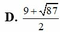
cho x+y+z thỏa mãn đẳng thức 4x^2 + 9y^2 + 16z^2 - 4x - 6y - 8z + 3 = 0
khi đó xy+yz+zx=
Cho x, y, z là 3 số thực dương và thoả mãn: \(4x^2+9y^2+16z^2=1\). Tìm giá trị nhỏ nhất của biểu thức: \(A=\dfrac{2x}{9y^2+16z^2}+\dfrac{3y}{4x^2+16z^2}+\dfrac{4z}{4x^2+9y^2}\)
Áp dụng bđt Svác xơ, ta có:
\(A\ge\dfrac{\left(\sqrt{2x}+\sqrt{3y}+\sqrt{4z}\right)^2}{2\left(4x^2+9y^2+16z^2\right)}\)\(=\dfrac{2x+3y+4z+2\left(\sqrt{6xy}+\sqrt{12yz}+\sqrt{8xz}\right)}{2}\)\(\ge\dfrac{1+2\left(3\sqrt[3]{\sqrt{576x^2y^2z^2}}\right)}{2}\)(BĐT Cô-si)\(\ge\dfrac{1+6}{2}=\dfrac{7}{2}\)
Vậy Amin=\(\dfrac{7}{2}\Leftrightarrow\)\(\left\{{}\begin{matrix}\dfrac{2x}{9y^2+16z^2}=\dfrac{3y}{4x^2+16z^2}=\dfrac{4z}{4x^2+9y^2}\\\sqrt{6xy}=\sqrt{12yz}=\sqrt{8xz}\end{matrix}\right.\)\(\Leftrightarrow x=\dfrac{3}{2}y=2z\)
Viết lại bài toán: Cho \(a^2+b^2+c^2=1\). Tìm max \(\sum\dfrac{a}{b^2+c^2}\)
với a=2x, b=3y, c=4z.
Áp dụng BĐT AM-GM:
\(a\left(b^2+c^2\right)=\dfrac{1}{\sqrt{2}}\sqrt{2a^2\left(1-a^2\right)\left(1-a^2\right)}\le\dfrac{1}{\sqrt{2}}\sqrt{\dfrac{8}{27}}=\dfrac{2}{3\sqrt{3}}\)
Do đó \(VT\ge\dfrac{3\sqrt{3}}{2}\left(a^2+b^2+c^2\right)=\dfrac{3\sqrt{3}}{2}\)
Vậy \(A_{Min}=\dfrac{3\sqrt{3}}{2}\)
1)a,b,c >0 ; a+b+c=1. CMR:
\(\dfrac{a}{1+a}\) + \(\dfrac{2b}{2+b}\) +\(\dfrac{3c}{c+3}\) \(\le\) \(\dfrac{6}{7}\)
2) x,y,z >0; 4x+9y+16z=49
CMR: \(\dfrac{1}{x}\) + \(\dfrac{25}{y}\) + \(\dfrac{64}{z}\) \(\ge\) 49
Từ \(\dfrac{a}{1+a}+\dfrac{2b}{2+b}+\dfrac{3c}{3+c}\le\dfrac{6}{7}\)
\(\Leftrightarrow1-\dfrac{a}{1+a}+2-\dfrac{2b}{2+b}+3-\dfrac{3c}{3+c}\ge6-\dfrac{6}{7}\)
\(\Leftrightarrow\dfrac{1}{a+1}+\dfrac{4}{b+2}+\dfrac{9}{c+3}\ge\dfrac{36}{7}\)
Áp dụng BĐT Cauchy-Schwarz dạng Engel ta có:
\(VT=\dfrac{1}{a+1}+\dfrac{4}{b+2}+\dfrac{9}{c+3}\)
\(\ge\dfrac{\left(1+2+3\right)^2}{a+b+c+6}=\dfrac{36}{7}=VP\)
Xảy ra khi \(a=\dfrac{1}{6};b=\dfrac{1}{3};c=\dfrac{1}{2}\)
2) \(\dfrac{1}{x}+\dfrac{25}{y}+\dfrac{64}{z}=\dfrac{4}{4x}+\dfrac{225}{9y}+\dfrac{1024}{16z}\ge\dfrac{\left(2+15+32\right)^2}{4x+9y+6z}=49\)
Cho x,y,z,t là các số nguyên dương thỏa mãn x+z=y+t và xz+1=yt . CMR y=t và x,y,z là 3 số nguyên liên tiếp .
Giúp mik với , làm được hôm nay cho 3 tik
từ câu a) ta có: \(\orbr{\begin{cases}x=y+1\\x=y-1\end{cases}}\) và \(\hept{\begin{cases}x-y=t-z\\y=t\end{cases}}\) (3)
+) Với \(x=y+1\) thì (3) \(\Leftrightarrow\)\(\hept{\begin{cases}y+1-y=y-z\\y=t\end{cases}}\Leftrightarrow\hept{\begin{cases}y=z+1\\y=t\end{cases}}\)
\(\Rightarrow\)\(x=y+1=z+2\) ( x,y,z là 3 số nguyên liên tiếp )
+) Với \(x=y-1\) thì (3) \(\Leftrightarrow\)\(\hept{\begin{cases}y-1-y=y-z\\y=t\end{cases}}\Leftrightarrow\hept{\begin{cases}y=z-1\\y=t\end{cases}}\)
\(\Rightarrow\)\(x=y-1=z-2\) ( x,y,z là 3 số nguyên liên tiếp )
\(x+z=y+t\)\(\Leftrightarrow\)\(x^2+z^2+2xz=y^2+t^2+2yt\) (1)
Mà \(xz+1=yt\)\(\Leftrightarrow\)\(2xz+2=2yt\)
(1) \(\Leftrightarrow\)\(x^2+z^2+2yt=y^2+t^2+2xz+4\)
\(\Leftrightarrow\)\(\left(x-z\right)^2-\left(y-t\right)^2=4\)
\(\Leftrightarrow\)\(\left(x-z-y+t\right)\left(x-z+y-t\right)=4\) (2)
Lại có: \(x+z=y+t\)\(\Rightarrow\)\(\hept{\begin{cases}x-y=t-z\\x-t=y-z\end{cases}}\)
(2) \(\Leftrightarrow\)\(\left(x-y\right)\left(x-t\right)=1\)
TH1: \(\hept{\begin{cases}x-y=1\\x-t=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=y+1\\x=t+1\end{cases}}\Leftrightarrow y=t\)
TH2: \(\hept{\begin{cases}x-y=-1\\x-t=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=y-1\\x=t-1\end{cases}}\Leftrightarrow y=t\)